Công thức tính cạnh tam giác vuông [chuẩn nhất] & kèm bài giải
Cạnh huyền trong tam giác là gì?
Cạnh huyền là tên của cạnh trong tam giác. Ngoài ra, trong một tam giác vuông, cạnh huyền đối diện với góc vuông.
» Tham khảo: HTTL.COM.VN
Khái niệm cạnh huyền trong tam giác vuông
Cạnh huyền là tên của cạnh trong tam giác vuông.
Trong một tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền. Đây cũng là cạnh dài nhất trong 3 cạnh của một tam giác vuông.
Hai cạnh còn lại gọi là cạnh góc vuông.
![Công thức tính cạnh tam giác vuông [chuẩn nhất]](https://truongxaydunghcm.edu.vn/wp-content/uploads/2022/02/cong-thuc-tinh-canh-tam-giac-vuong.jpg)
Cách để tìm chiều dài cạnh huyền (công thức tính cạnh tam giác vuông cân khi biết cạnh huyền)
Mọi tam giác vuông đều có một góc vuông (90 độ) và cạnh huyền là cạnh còn lại hoặc cạnh dài nhất của tam giác vuông. Cạnh huyền là cạnh dài nhất của một tam giác vuông và có thể dễ dàng tìm độ dài cạnh này bằng một số phương pháp khác nhau. Bài viết dưới đây sẽ hướng dẫn các bạn công thức tính cạnh trong tam giác vuông, vuông cân sử dụng định lý Pitago & các phương pháp khác để biết độ dài hai cạnh còn lại của tam giác vuông.
Tiếp theo, bạn sẽ học cách xác định cạnh huyền của một số tam giác vuông đặc biệt thường xuất hiện trong đề thi. Cuối cùng, bạn sẽ làm quen với cách sử dụng định lý Sin để tìm độ dài cạnh huyền khi chỉ biết độ dài của một cạnh và số đo của góc nhọn.
Phương pháp 1 :Sử dụng định lý Pytago
- Công thức tính cạnh tam giác vuông cân khi biết cạnh huyền

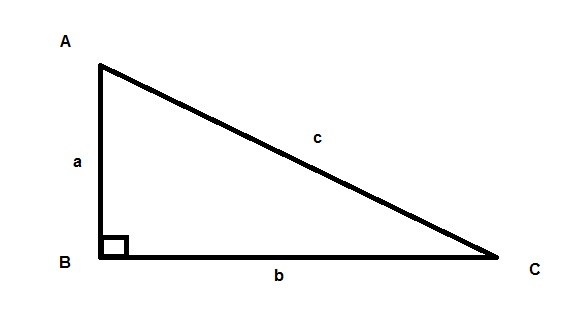
 Học định lý Pytago. Định lý Pytago mô tả mối quan hệ giữa các cạnh của một tam giác vuông.[2] Nó nói rằng với một tam giác vuông bất kỳ có chiều dài hai cạnh góc vuông lần lượt là a và b, chiều dài cạnh huyền là c, ta có: a2 + b2 = c2.[3]
Học định lý Pytago. Định lý Pytago mô tả mối quan hệ giữa các cạnh của một tam giác vuông.[2] Nó nói rằng với một tam giác vuông bất kỳ có chiều dài hai cạnh góc vuông lần lượt là a và b, chiều dài cạnh huyền là c, ta có: a2 + b2 = c2.[3] 

Đảm bảo rằng tam giác của bạn là tam giác vuông. Định lý Pytago chỉ đúng với tam giác vuông, và theo định nghĩa, chỉ tam giác vuông mới có cạnh huyền. Nếu tam giác của bạn có chứa một góc có số đo đúng bằng 90 độ, nó là tam giác vuông và bạn có thể tiếp tục.
- Góc vuông thường được ký hiệu trong sách giáo khoa và trong các bài kiểm tra bằng một góc vuông nhỏ nằm ở góc của góc. Dấu hiệu đặc biệt này nghĩa là “90 độ”.


Gán biến a, b và c vào các cạnh trong tam giác của bạn. Biến “c” luôn được dùng cho cạnh huyền – cạnh dài nhất. Chọn một trong hai cạnh còn lại là a và gọi cạnh còn lại là b (cạnh nào là a và cạnh nào là b không quan trọng, tính toán sẽ cho ta kết quả như nhau). Tiếp đó, thay chiều dài của a và b vào công thức, như ví dụ dưới đây:
- Nếu tam giác của bạn có hai cạnh góc vuông là 3 và 4, và bạn đã đặt tên cho những cạnh đó lần lượt là a = 3 và b = 4, vậy phương trình của chúng ta sẽ là: 32 + 42 = c2.


Tìm bình phương của a và b. Để tìm bình phương của một số, bạn chỉ việc lấy số đó nhân với chính nó, nghĩa là a2 = a x a. Hãy tìm bình phương của cả a và b, và viết vào công thức của bạn.
- Nếu a = 3, a2 = 3 x 3, hay 9. Nếu b = 4, vậy b2 = 4 x 4, hay 16.
- Thay các giá trị vào, ta có phương trình như sau: 9 + 16 = c2.


Cộng các giá trị a2 và b2 với nhau. Thay vào phương trình, ta sẽ có giá trị của c2. Chỉ còn lại một bước cuối cùng, và bạn sẽ có được chiều dài của cạnh huyền!
- Trong ví dụ của chúng ta: 9 + 16 = 25, do đó, bạn có thể viết 25 = c2.


Tìm căn bậc hai của c2. Sử dụng chức năng căn bậc hai trong máy tính bỏ túi của bạn (hoặc những gì trong bảng cửu chương mà bạn nhớ được) để tìm căn bậc hai của c2. Câu trả lời chính là chiều dài cạnh huyền của bạn!
- Trong ví dụ: c2 = 25. Căn bậc hai của 25 là 5 (5 x 5 = 25, nên Sqrt(25) = 5). Nghĩa là c = 5 – chiều dài cạnh huyền!
Phương pháp 2 :Tìm cạnh tam giác vuông đặc biệt
Tìm cạnh tam giác vuông đặc biệt


Học cách nhận biết Tam giác Bộ ba số Pytago. Chiều dài các cạnh trong một tam giác bộ ba số Pytago là những số nguyên đáp ứng định lý Pytago. Những tam giác đặc biệt này thường xuyên xuất hiện trong sách giáo khoa hình học và những bài thi chuẩn hóa, chẳng hạn như SAT hay GRE. Nếu có thể học thuộc, đặc biệt là hai bộ ba số Pytago đầu tiên, bạn có thể tiết kiệm được rất nhiều thời gian khi làm bài, bởi lúc đó, chỉ bằng cách nhìn vào chiều dài các cạnh góc vuông của chúng, bạn có thể biết ngay chiều dài cạnh huyền của một trong những tam giác này! [4]
- Bộ ba số Pytago đầu tiên là 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Khi thấy một tam giác vuông có hai cạnh góc vuông lần lượt là 3 và 4, bạn có thể xác định được ngay mà không cần phải tính toán gì rằng nó có cạnh huyền bằng 5.
- Tỉ lệ của bộ ba số Pytago vẫn đúng, kể cả khi các cạnh được nhân với một số khác. Chẳng hạn như, tam giác vuông có chiều dài hai cạnh góc vuông là 6 và 8 sẽ có chiều dài cạnh huyền là 10 (62 + 82 = 102, 36 + 64 = 100). Tương tự với 9-12-15, hay thậm chí 1,5-2-2,5. Hãy thử đặt phép tính và tự mình kiểm chứng!
- Bộ ba số Pytago thường xuất hiện trong các bài kiểm tra là 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Bạn cũng hãy để ý những bộ bội số như 10-24-26 hay 2,5-6-6,5.
- Công thức tính cạnh tam giác vuông cân


Ghi nhớ tỉ lệ các cạnh của tam giác vuông cân 45-45-90. Tam giác vuông 45-45-90 là tam giác có ba góc lần lượt là 45, 45 và 90 độ, còn được gọi là Tam giác Vuông Cân. Tam giác vuông cân thường xuyên xuất hiện trong các bài thi chuẩn hóa và là dạng tam giác rất dễ giải. Cạnh của tam giác này có tỉ lệ 1:1:Sqrt(2), nghĩa là hai cạnh góc vuông bằng nhau và chiều dài cạnh huyền đơn giản là bằng chiều dài cạnh góc vuông nhân với căn bậc hai của hai.
- Để tính cạnh huyền của một tam giác dựa vào chiều dài của một cạnh góc vuông, ta chỉ việc lấy chiều dài cạnh góc vuông đó nhân với Sqrt(2).[5]
- Việc nắm được tỉ lệ này sẽ trở nên vô cùng hữu dụng, đặc biệt là khi câu hỏi kiểm tra hay bài tập cho bạn chiều dài cạnh góc vuông theo biến thay vì số nguyên.


Học tỉ lệ các cạnh của tam giác vuông 30-60-90. Đây là tam giác có số đo các góc lần lượt là 30, 60 và 90 độ, và tam giác này xuất hiện khi bạn chia đôi một tam giác đều. Các cạnh của tam giác vuông 30-60-90 luôn giữ tỉ lệ 1:Sqrt(3):2, hay x:Sqrt(3)x:2x. Nếu cho biết chiều dài một cạnh góc vuông của tam giác vuông 30-60-90 và yêu cầu tìm chiều dài cạnh huyền, đó sẽ là một bài toán rất dễ:[6]
- Nếu bài toán cho biết chiều dài cạnh góc vuông ngắn hơn (đối diện góc 30 độ), bạn chỉ việc nhân đôi chiều dài cạnh đó để tìm chiều dài cạnh huyền. Chẳng hạn như, nếu chiều dài cạnh góc vuông ngắn hơn là 4, bạn biết rằng chiều dài cạnh huyền phải là 8.
- Nếu bài toán cho biết chiều dài cạnh góc vuông dài hơn (đối diện góc 60 độ), hãy nhân chiều dài cạnh đó với 2/Sqrt(3) để tìm chiều dài cạnh huyền. Ví dụ như, nếu chiều dài cạnh góc vuông dài hơn 4, bạn biết rằng chiều dài cạnh huyền phải là 4,62.
Phương pháp 3 :Tìm cạnh huyền bằng định lý Sin

 Hiểu “Sin” nghĩa là gì. Những thuật ngữ “sin”, “cosin” và “tang” đều được dùng để chỉ những tỉ số khác nhau giữa các góc và/hoặc các cạnh của một tam giác vuông. Trong một tam giác vuông, sin của một góc được xác định bằng chiều dài của cạnh đối diện chia cho cạnh huyền. Trong phương trình và máy tính bỏ túi, sin đều được ký hiệu là sin.[7]
Hiểu “Sin” nghĩa là gì. Những thuật ngữ “sin”, “cosin” và “tang” đều được dùng để chỉ những tỉ số khác nhau giữa các góc và/hoặc các cạnh của một tam giác vuông. Trong một tam giác vuông, sin của một góc được xác định bằng chiều dài của cạnh đối diện chia cho cạnh huyền. Trong phương trình và máy tính bỏ túi, sin đều được ký hiệu là sin.[7]
 Học cách tính sin. Kể cả máy tính khoa học cơ bản cũng có chức năng sin. Hãy tìm phím có ký hiệu sin. Để tìm sin của một góc, thường thì bạn sẽ phải nhấn phím sin rồi nhập số đo góc theo đơn vị độ. Tuy nhiên, ở một số máy tính, bạn sẽ phải nhập số đo độ trước rồi mới đến phím sin. Bạn sẽ phải thử nghiệm trên máy tính hoặc kiểm tra hướng dẫn sử dụng để xác định đâu là cách đúng.
Học cách tính sin. Kể cả máy tính khoa học cơ bản cũng có chức năng sin. Hãy tìm phím có ký hiệu sin. Để tìm sin của một góc, thường thì bạn sẽ phải nhấn phím sin rồi nhập số đo góc theo đơn vị độ. Tuy nhiên, ở một số máy tính, bạn sẽ phải nhập số đo độ trước rồi mới đến phím sin. Bạn sẽ phải thử nghiệm trên máy tính hoặc kiểm tra hướng dẫn sử dụng để xác định đâu là cách đúng.- Để tìm sin của một góc 80 độ, bạn sẽ phải bấm sin 80 rồi dấu bằng hay phím enter hoặc 80 sin (Đáp án là -0,9939).
- Bạn cũng có thể gõ “sine calculator” (máy tính sin) vào một công cụ tìm kiếm và tìm vô số máy tính dễ sử dụng để không phải có bất kỳ sự phỏng đoán nào nữa.[8]


Học định lý Sin. Định lý Sin là một công cụ hữu dụng trong việc giải bài toán tam giác. Cụ thể là, nó sẽ giúp bạn tìm cạnh tam giác vuông khi biết chiều dài một cạnh góc vuông và số đo một góc khác, bên cạnh góc vuông. Với mọi tam giác có các cạnh a, b, và c, và các góc A, B, và C, định lý Sin nói rằng a / sin A = b / sin B = c / sin C.[9]
- Định lý Sin thật sự có thể được dùng để giải mọi tam giác, nhưng chỉ tam giác vuông mới có cạnh huyền.

 Gán biến a, b, và c cho các cạnh trong tam giác của bạn. Cạnh huyền (dài nhất) phải là “c”. Để đơn giản, ta đặt cạnh đã biết là “a” và cạnh còn lại là “b”. Tiếp đến, gán các biến A, B, và C cho các góc của tam giác. Góc vuông đối diện cạnh huyền sẽ là “C”. Đối diện cạnh “a” là góc “A” và đối diện cạnh “b” là “B”.
Gán biến a, b, và c cho các cạnh trong tam giác của bạn. Cạnh huyền (dài nhất) phải là “c”. Để đơn giản, ta đặt cạnh đã biết là “a” và cạnh còn lại là “b”. Tiếp đến, gán các biến A, B, và C cho các góc của tam giác. Góc vuông đối diện cạnh huyền sẽ là “C”. Đối diện cạnh “a” là góc “A” và đối diện cạnh “b” là “B”.

Tính số đo góc thứ ba. Bởi đó là tam giác vuông, bạn đã biết C = 90 độ, và bạn cũng đã biết số đo của A hoặc B. Bởi tổng số đo ba góc trong của một tam giác luôn bằng 180 độ, bạn có thể dễ dàng tính được số đo góc thứ ba bằng công thức sau: 180 – (90 + A) = B. Bạn cũng có thể đảo ngược phương trình như 180 – (90 + B) = A.
- Ví dụ, nếu đã biết A = 40 độ, vậy B = 180 – (90 + 40). Thu gọn về B = 180 – 130, và ta có thể nhanh chóng xác định B = 50 độ.


Kiểm tra tam giác của bạn. Đến thời điểm này, hẳn là bạn phải biết số đo của cả ba góc và chiều dài cạnh a. Giờ là lúc thay thông tin vào phương trình định lý Sin nhằm xác định chiều dài hai cạnh còn lại.
- Để tiếp tục ví dụ, giả sử chiều dài của cạnh a = 10. Góc C = 90 độ, góc A = 40 độ và góc B = 50 độ.

 Áp dụng định lý Sin cho tam giác của bạn. Ta chỉ cần thay số vào và giải phương trình sau để tìm cạnh huyền c: chiều dài cạnh a / sin A = chiều dài cạnh c / sin C. Trông vẫn còn khá đáng sợ, nhưng sin của 90 độ là một hằng số và luôn bằng 1! Do đó, phương trình có thể được thu gọn thành: a / sin A = c / 1, hay chỉ đơn giản là a / sin A = c.
Áp dụng định lý Sin cho tam giác của bạn. Ta chỉ cần thay số vào và giải phương trình sau để tìm cạnh huyền c: chiều dài cạnh a / sin A = chiều dài cạnh c / sin C. Trông vẫn còn khá đáng sợ, nhưng sin của 90 độ là một hằng số và luôn bằng 1! Do đó, phương trình có thể được thu gọn thành: a / sin A = c / 1, hay chỉ đơn giản là a / sin A = c.

Chia chiều dài cạnh a cho sin góc A để tìm chiều dài cạnh huyền! Bạn có thể thực hiện trong hai bước riêng biệt, đầu tiên là tính sin A và viết ra giấy, rồi tiếp đến lấy a chia cho kết quả đó. Hoặc bạn có thể cùng lúc nhập tất cả vào máy tính. Nếu làm vậy, đừng quên dùng ngoặc đơn sau dấu chia. Chẳng hạn như, bấm 10 / (sin 40) hoặc 10 / (40 sin), tùy vào máy tính của bạn.
- Với ví dụ của chúng ta, ta tìm được sin 40 = 0,64278761. Để tìm giá trị của c, ta chỉ việc chia chiều dài của a cho số này, và có được 10 / 0,64278761 = 15,6 – chiều dài cạnh huyền!
Công thức cách tính cạnh tam giác vuông theo công thức lượng giác
Độ dài các cạnh và góc trong một tam giác vuông có mối quan hệ chặt chẽ với nhau. Đây cũng chính là các đại lượng làm tiền đề cho những công thức lượng giác. Vậy dựa vào các công thức lượng giác, chúng ta có thể tìm được chiều dài của cạnh huyền góc vuông hay không? Câu trả lời sẽ có ngay sau đây.
Sin được dùng để chỉ tỉ số giữa các góc hoặc các cạnh trong tam giác vuông. Trong một tam giác vuông, sin của một góc được xác định bằng chiều dài của cạnh đối diện chia cho cạnh huyền.
Với mọi tam giác có cạnh a,b,c và các góc A, B, C thì theo định lý Sin ta có
a / sinA = b / sinB = c / sinC
Định lý Sin có thể dùng để giải mọi tam giác, nhưng để tính cạnh huyền thì chỉ có tam giác vuông mới có.
Bài tập về tính cạnh tam giác vuông và vuông cân [tham khảo]
Bài tập 1: Một tam giác vuông có chiều dài bằng 10cm, cạnh bên bằng 6cm. Hỏi cạnh còn lại bằng bao nhiêu?
Lời giải
Áp dụng công thức tính cạnh trong tam giác ở trên ta có:
a = 6cm, c = 10cm
=> c2 = a2 + b2
102 = 62 + b2
100 = 36 + b2
Xem Thêm : Mẫu báo cáo tiến độ công việc mới nhất và 4 bước cơ bản để xây dựng
B2 = 100 – 36
B2 = 64
B = 8cm
Đáp số: 8cm
Bài tập 2: Cho ∆MNP vuông tại M, biết MN = 6cm, MP = 8cm. Hỏi NP bằng bao nhiêu?
Lời giải
Theo định lý pytago ta có:
a = MN = 6cm, b = MP = 8cm
c2 = a2 + b2
= 62 + 82
= 36 + 64
= 100
=> c = 10cm
=> NP = 10cm
Đáp số: 10cm
Bài tập 3 : Cho ∆ABC vuông tại B, có AB bằng 8 cm, BC bằng 10cm. Hãy tính chiều dài cạnh huyền AC
Lời giải :
Áp dụng công thức cách tính cạnh tam giác vuông theo định lý Pitago thì ta có :
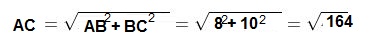
=> AC = 12,8 cm
Vậy độ dài cạnh tam giác vuông ABC đó là : 12,8 cm
Bài tập 4:
Một tam giác vuông có chiều dài 2 cạnh góc vuông lần lượt bằng 15cm, cạnh bên bằng 9cm. Hỏi cạnh còn lại bằng bao nhiêu?
Lời giải
Áp dụng định lý pitago trong cách tính cạnh huyền thì ta có :
a = 9cm, b = 15cm
=> c2 = a2 + b2
c2 = 92 + 152
c2 = 81 + 225
c2 = 306
=> c = 17,5cm
Xem Thêm : Các cấu trúc viết lại câu Tiếng Anh thông dụng nhất và Bài tập
Vậy độ dài cạnh huyền c của tam giác vuông là : 17,5 cm
Bài tập 5:
Cho ∆MNP vuông tại M, biết MN = 8cm, MP = 12cm. Hỏi NP bằng bao nhiêu?
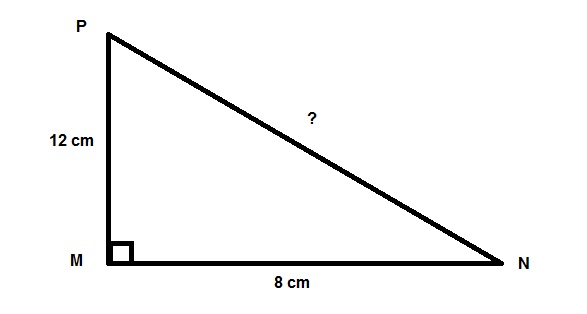
Lời giải
Theo định lý pytago ta có:
MN = 8cm, MP = 12 cm
NP2 = 82 + 122
NP2 = 64 + 144
NP2 = 208
=> Độ dài cạnh huyền là : NP = 14,5 cm
Bài tập 6:
Chọn tam giác nhọn ABC. Kẻ AH vuông góc với BC (H ∈ BC) Cho biết AB = 15 cm, AH = 14cm, HC = 15cm. Tính các độ dài AC, BC.
Bài giải :
ΔAHC vuông tại H nên theo Định lí Py-ta-go
AC² = AH² + HC² = 14² + 15²
= 196 + 225 = 421
Do đó AC = 20,5 cm
ΔAHB vuông tại H nên:
BH² = AB² – AH² = 15² – 14² = 225 – 196 = 29
Vậy BH = 5,3 cm.
Bài tập 7:
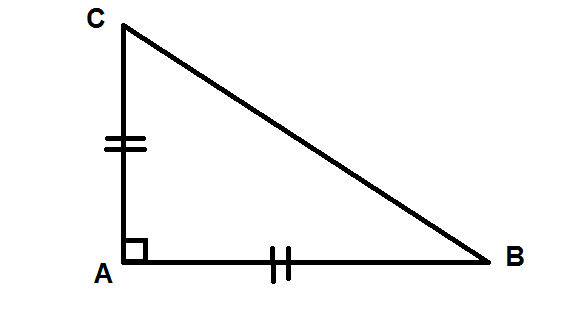
Cho tam giác ABC , vuông tại A . Tính cạnh huyền và diện tích của một tam giác vuông cân nếu a là cạnh góc vuông.\
Hướng dẫn giải:
Xét tam giác ABC vuông cân tại A có AB = AC = a.
Áp dụng định lý Py – ta – go ta có:
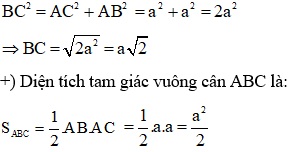
Bài tập 8:
(công thức tính cạnh tam giác vuông cân khi biết cạnh huyền)
Như vậy việc tính cạnh tam giác vuông thật dễ dàng phải không các bạn. Bạn chỉ cần áp dụng định lý Pitago một cách chính xác để giải quyết vấn đề này. Các bạn hãy học thuộc để nhớ công thức tính cạnh tam giác vuông và luyện tập nhiều nhé. TRUONGXAYDUNGHCM.EDU.VN hy vọng bạn có một bài học tốt.
THAM KHẢO:
- Top 10 địa chỉ Spa chăm sóc da mặt uy tín nhất TPHCM
- Top 5 Spa tắm trắng uy tín hiệu quả bậc nhất tại TPHCM
- Top 5 Spa Gò Vấp chuyên làm đẹp và chăm sóc da tại TPHCM
- Top 15 địa chỉ phun xăm thẩm mỹ uy tín chất lượng nhất TPHCM
- TOP 8 spa bình thạnh làm đẹp uy tín tốt nhất HCM
Nguồn: https://truongxaydunghcm.edu.vn
Danh mục: Công thức



