Giải bài 23,24,25 ,26,27,28 ,29,30 trang 66,67 SGK Toán 7 tập 2: Tính chất ba đường trung tuyến của tam giác

công bố 4 tính chất của ba trung tuyến của một tam giác: giải bài 23,24 trang 66; bài 25,26,27,28,29,30 trang 67 SGK toán 7 tập 2 hình học chương 3.

23. gọi g là trọng tâm của Δdef với đường trung trực dh. Câu nào sau đây là đúng?

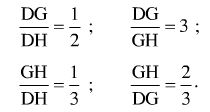
g là tâm của Δdef với đường trung bình dh. Câu đúng là:

24. cho hình ảnh bên. Điền các số thích hợp vào chỗ trống trong các phương trình sau:

a) mg =… thưa ông; gr =… thưa ngài; gr =… mg

b) ns = ..ng; ns =… gs; ng = gs

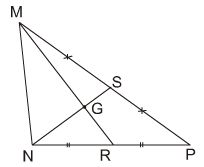
Hình bên cho chúng ta biết rằng hai trung tuyến mr và ns cắt nhau tại g, do đó g là trọng tâm của tam giác. thì chúng ta nhập số như sau:

bài 25 trang 67. biết rằng: trong một hình vuông, đường trung tuyến cạnh nó bằng nửa cạnh huyền. giải quyết vấn đề sau:

cho Δsquare abc có hai cạnh ab = 3 cm, ac = 4 cm. tính khoảng cách từ đỉnh a đến trọng tâm g của abc.

hướng dẫn: ∆abc bình phương trong a = & gt; bc2 = ab2 + ac2

bc2 = 32 + 42

bc2 = 25

bc = 5

gọi m là trung điểm của bc = & gt; am là trung vị với cạnh huyền bằng nửa cạnh huyền nên am = 1/2 bc

vì g là trọng tâm của abc nên:

26. chứng minh định lý: trên một tỉ lệ, hai trung tuyến có hai cạnh bằng nhau.

Giả sử abc cân bằng tại a có hai trung tuyến bm và cn, ta chứng minh bm = cn

chúng tôi có một = nb = ab / 2 (thuộc tính đường trung bình)

am = mc = ac / 2 (thuộc tính đường giữa)

vì ∆abc có trọng số tại a = & gt; ab = ac so am = an

xem xét bam; ∆m có thể có:

am = a (cm ở trên)

Xem thêm: Hướng Dẫn Sử Dụng Tay Cầm Ps4 Trên Máy Tính Pc Hiệu Q Belibo Store

góc chung

ab = ac (∆abc trọng lượng)

nên suy ra bam = can (c-g-c)

= & gt; bm = cn (2 cạnh tương ứng)

bài 27. Chứng minh điều ngược lại với định lý trước: nếu Δ có hai trung tuyến bằng nhau thì Δ bằng nhau.

giả sử abc có hai trung bình là be và cf nằm trong g

= & gt; g là trọng tâm của

Xem Thêm : Hướng Dẫn Lập Trình Cnc Từ A Đến Z, Lập Trình Cnc Cơ Bản

= & gt; gb = 2/3 được; gc = 2/3 cf

đó là = cf (đoán) nên gb = gc

= & gt; ∆gbc được cân bằng g = & gt; gcb = gbc

xem xét rằng bgf và cge có:

gb = gc (cmt)

angle bgf = angle cge (2 góc đối diện)

ge = gf

⇒ bgf = cge (c-g-c)

⇒ bf = ce (2 cạnh tương ứng)

xem xét Δfbc và Δecb trong đó bf = ce (cmt) cạnh bc chung be = cf (gt)

⇒ Δfbc = Δecb (c-c-c) ⇒ góc b = góc c coi Δabc có góc b = góc c ⇒ Δabc là Δ cân tại a. (2 góc dưới bằng nhau)

bài tập 28. cho Δdef bằng d với di trung vị

a) thử dei = dfi

b) góc ma trận và góc vi phân là gì?

c) Biết rằng = df = 13cm, ef = 10cm, hãy tính độ dài trung tuyến.

lời giải: a) ∆dei = ∆dfi có:

di là biên giới chung

de = df (số dư def)

tức là = if (di là median.line)

Xem thêm: List Phi Luật Tân là nước nào và ở đâu?

= & gt; ∆dei = ∆dfi (c.c.c)

b) vì ∆dei = ∆dfi = & gt; die = diff

trong đó die + diff = 1800 (liền kề)

sau đó die = diff = 900

c) i là trung điểm của ef ví dụ = si = 5 cm

∆dei vuông tại i = & gt; di2 = de2 – ei2 (Định lý Pitago)

= & gt; di2 = 132 – 52 = 144

= & gt; say = 12

bài 29 trang 67. gọi g là trọng tâm của Δall abc. cho thấy rằng:

ga = gb = gc

đặt m, n, e là giao của ag, bg, cg với bc, ca, ab.

vì g là trọng tâm của abc

vì ∆abc đều nên ba trung tuyến của đoạn thẳng ứng với ba cạnh bc, ca, ab bằng nhau

= & gt; am = bn = ce (2)

trong tổng số (1), (2) = & gt; ga = gb = gc

bài 30 trang 67 sgk toán 7: gọi g là trọng tâm của Δabc. trên tia ag lấy một điểm g ‘sao cho g là trung điểm của ag’

a) so sánh các cạnh của bgg ‘với các trung tuyến của Δabc

b) so sánh các trung tuyến của Δbgg ‘với các cạnh của Δabc.

Xem Thêm : Hướng Dẫn Sử Dụng Phần Mềm Dumpper 91, #1 Cách Sử Dụng Dumpper

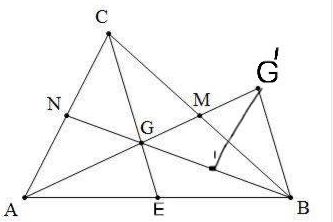
a) so sánh các cạnh của bgg ‘với các trung tuyến của abc bg cắt ac tại n

cg cắt ab thành e

g là trọng tâm của abc

= & gt; ga = 2/3 giờ sáng

trong đó ga = gg ‘(g là điểm giữa của ag’)

gg ‘= 2/3 a. m.

vì g là trọng tâm của ∆abc = & gt; GB = 2/3 nghìn tỷ

ngược lại: gm = 1/2 ag (g là trọng tâm)

Xem thêm: Tiền sử dụng đất là gì?

ag = gg ‘(gt)

gr = 1/2 g ’

m là trung điểm gg ‘

so gmc = g’mb vì:

gm = mg ‘

mb = mc

∠gmc = g’mb

= & gt; bg ‘= cg

trong đó cg = 2/3 ce (g là abc centroid)

= & gt; bg ‘= 2/3 ce

thì mỗi cạnh của bgg ‘bằng 2/3 đường trung bình của ∆abc

b) so sánh các đường trung bình của ∆bgg ‘với cạnh ∆abc

chúng ta có: bm là bgg trung vị ‘

trong đó m là trung điểm của bc nên bm = 1/2 bc

vì ig = 1/2 bg (tôi là trung điểm của bg)

gn = 1/2 bg (g là trọng tâm)

= & gt; ig = gn

do đó ∆igg ‘= ∆nga (cgc) = & gt; ig ‘= an = & gt; ig ‘= ac / 2

– gọi k là trung điểm bg = & gt; gk là đường trung bình ∆bgg ‘

vì ge = 1/2 gc (g là abc centroid)

= & gt; g = 1/2 g

trong đó k là trung điểm bg ‘= & gt; kg ‘= chẳng hạn

vì gmc = g’bm (đã chứng minh ở trên)

= & gt; ∠gcm = ∠g’bm (góc bên trong của đế lại)

= & gt; ce // bg ‘= & gt; age = ag’b (đồng vị)

do đó ∆age = ∆gg’k (cgc) = & gt; ae = gk

rằng ae = 1/2 ab thì gk = 1/2 ab

khi đó mỗi trung vị bgg ‘là một nửa cạnh của abc song song với nó