Bài 4. Phân tích tương quan Pearson r (Pearsons Correlation r)

Phân tích tương quan pearson r (cung cấp hệ số tương quan pearson, được gọi là r ) là một phép đo sức mạnh của mối liên kết tuyến tính giữa hai biến. Về cơ bản, mối tương quan của Pearson cố gắng vẽ một đường phù hợp nhất thông qua dữ liệu hai biến và hệ số tương quan Pearson, r, cho biết khoảng cách của tất cả các điểm dữ liệu này so với đường phù hợp nhất này (tức là các điểm dữ liệu này tốt đến mức nào với mẫu / dòng mới phù hợp nhất).

1. khi nào sử dụng?

phân tích tương quan của pearson, r, có thể được sử dụng làm công cụ ước lượng mẫu cho tương quan dân số, ρ (rho). là một chỉ số không có thứ nguyên về mối quan hệ tuyến tính giữa hai biến ngẫu nhiên, giá trị 0 có nghĩa là không có mối quan hệ tuyến tính giữa các biến và giá trị 1 cho thấy mối quan hệ tuyến tính hoàn hảo. nếu mối tương quan là âm, có nghĩa là sự gia tăng giá trị của một biến được kết hợp với giá trị hàm mũ của biến kia. giá trị của r có thể thay đổi giữa −1 và +1 bất kể kích thước đo lường của hai biến.

Tương quan của Pearson, r, nên được coi là một thống kê mô tả khi một nhà nghiên cứu muốn định lượng mức độ của mối quan hệ tuyến tính giữa các biến. tương quan tham số sẽ thích hợp bất cứ khi nào các phép đo định lượng được thực hiện trên hai hoặc nhiều biến đồng thời, mối quan hệ giữa hai biến là tuyến tính và cả hai biến đều được phân phối bình thường. Các mối tương quan phải luôn được kiểm tra trước khi thực hiện các phân tích đa biến phức tạp hơn, chẳng hạn như phân tích nhân tố hoặc phân tích thành phần chính. Mức độ của mối quan hệ tuyến tính giữa hai biến có thể khó đánh giá từ biểu đồ phân tán và hệ số tương quan cung cấp một bản tóm tắt ngắn gọn hơn. tuy nhiên, không nên cố gắng tính toán mối tương quan khi biểu đồ phân tán cho thấy mối quan hệ phi tuyến tính rõ ràng. khi một nhà nghiên cứu quan tâm đến cả chiều rộng và tầm quan trọng của mối tương quan, thì r được sử dụng theo cách suy luận như một ước tính về mối tương quan dân số, (rho).

Công thức tính hệ số tương quan Pearson trong hai biến x và y của n mẫu như sau:

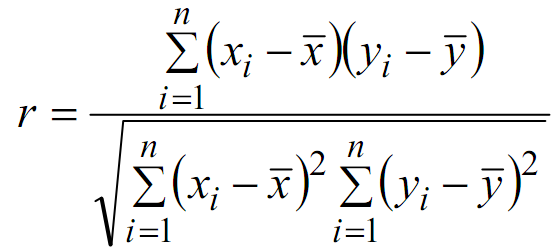
2. giả thuyết vô hiệu và suy luận thống kê

Khi ước tính quy mô của mối tương quan dân số, chúng tôi có thể muốn kiểm tra xem nó có ý nghĩa thống kê hay không. giả thuyết rỗng là h0: ρ = 0, tức là, biến x không liên quan tuyến tính với biến y. giả thuyết thay thế là h1: ρ ≠ 0. giả thuyết rỗng là một phép kiểm tra xem có bất kỳ mối quan hệ rõ ràng nào giữa các biến x và y có thể xuất hiện một cách tình cờ hay không. phân phối lấy mẫu của r không bình thường khi tương quan dân số lệch 0 và khi cỡ mẫu nhỏ (n <30). thì kiểm định ý nghĩa r được thay thế bằng một thống kê khác có tên là Fisher’s z .

3. giả định thống kê

Trong một số sách thống kê cho các nhà khoa học xã hội, người ta nói rằng để sử dụng mối tương quan của Pearson, cả hai biến số phải được phân phối chuẩn, nhưng trong các văn bản khác, nó nói rằng phân phối của cả hai biến số phải là đối xứng (đối xứng) và đơn phương nhưng không nhất thiết phải bình thường . những ý kiến ​​này gây ra sự hoang mang lớn trong giới nghiên cứu và cần được làm rõ. nếu thống kê tương quan chỉ được sử dụng cho mục đích mô tả, thì không cần sử dụng các giả định chuẩn về hình dạng của phân phối dữ liệu. các giả định duy nhất được yêu cầu là:

• các thước đo định lượng (khoảng hoặc mức thang đo của một phép đo) được thực hiện đồng thời trên hai hoặc nhiều biến ngẫu nhiên. có nghĩa là, hai biến số phải được đo lường trên một khoảng tỷ lệ hoặc thang đo. tuy nhiên, cả hai biến không cần phải được đo trên cùng một thang đo (ví dụ: một biến có thể là một tỷ lệ và biến kia có thể là một khoảng).
• các phép đo được ghép nối cho từng đối tượng (ví dụ: mỗi người tham gia) là sống độc lập. Ví dụ: bạn đã thu thập thời gian ôn tập (tính bằng giờ) và điểm kiểm tra (đo từ 0 đến 100) cho 100 sinh viên được chọn ngẫu nhiên tại một trường đại học (nghĩa là bạn có hai biến liên tục: “thời gian xem xét” và “đánh giá thành tích” ). mỗi người trong số 100 sinh viên sẽ có giá trị thời gian ôn tập (ví dụ: “sinh viên số 1” đã học trong “23 giờ”) và kết quả kiểm tra (ví dụ: “sinh viên số 1” đạt “81/100”). thì bạn sẽ có 100 giá trị được nối.

Kết quả thu được sẽ mô tả mức độ áp dụng mối quan hệ tuyến tính cho dữ liệu mẫu.

Hơn nữa, cần thận trọng khi sử dụng r . đây không phải là những giả định nghiêm ngặt, nhưng trong các tình huống nghiên cứu điển hình mà r nên được diễn giải một cách thận trọng hoặc không được sử dụng.

• Khi phương sai của hai thước đo rất khác nhau, thường liên quan đến các phạm vi khác nhau, hoặc có thể là một phạm vi giới hạn cho một biến, tương quan mẫu sẽ bị ảnh hưởng. ví dụ: nếu một biến bị giới hạn phạm vi (một phần của phạm vi điểm không được sử dụng hoặc không phù hợp), điều này sẽ có xu hướng làm giảm (thấp hơn) mối tương quan giữa hai biến.
• khi có các giá trị ngoại lệ, r nên được diễn giải một cách thận trọng.
• khi các quan sát được rút ra từ một nhóm không đồng nhất . tốt nhất, dữ liệu phải đồng nhất . tính đồng nhất trong mối tương quan có nghĩa là các phương sai dọc theo dòng phù hợp nhất vẫn tương tự khi bạn di chuyển dọc theo dòng. nếu các phương sai không giống nhau, thì có một phương sai thay đổi (còn được gọi là phương sai thay đổi ). tính đồng nhất (hoặc độ đàn hồi đồng đều) dễ được biểu diễn nhất bằng biểu đồ, như hình dưới đây:

• Khi dữ liệu thưa thớt (với rất ít phép đo), không nên sử dụng r . với rất ít giá trị, không thể nói mối quan hệ của hai biến là tuyến tính hay không. Tương quan r của pearson phù hợp hơn với các mẫu lớn hơn (n> 30).
• không nên được sử dụng khi các giá trị của một trong các biến đã được cố định.

li>

4. phân tích tương quan pearson r trong spss

Ví dụ: một nhà nghiên cứu muốn biết liệu kết quả của bài kiểm tra viết cuối kỳ môn toán giải thích có tương quan với thời gian học sinh dành cho bài đánh giá cuối cùng hay không. 20 sinh viên đã được mời tham gia một thí nghiệm, trong đó, từ khi kết thúc bài giải tích cho đến ngày thi cuối kỳ, họ được yêu cầu ghi lại tổng số giờ ôn tập (tích lũy cho mỗi ngày) dành cho môn toán. Khi kết thúc kỳ thi, nhà nghiên cứu đã thu thập điểm của 20 sinh viên này trên thang điểm 100 và tổng hợp lại theo bảng sau.

Xem thêm: Mẫu báo cáo tiến độ công việc mới nhất và 4 bước cơ bản để xây dựng

Hai câu hỏi nghiên cứu được xem xét: i) Điểm của bài kiểm tra viết cuối kỳ môn toán giải thích có liên quan tuyến tính với số giờ ôn tập của học sinh không? và ii) số giờ ôn tập của học sinh có liên quan tuyến tính đến điểm cuối cùng của bài kiểm tra viết trong môn toán giải thích không?

Các bước bên dưới cho chúng tôi biết cách phân tích mối tương quan r của Pearson trong thống kê spss.

– bước 1: Kiểm tra biểu đồ phân tán mô tả mối quan hệ giữa hai biến. đọc bài đăng về cách vẽ biểu đồ phân tán. kết quả của biểu đồ phân tán được hiển thị trong hình sau.

Xem Thêm : 7 công thức nước ép cải kale giúp da sáng dáng xinh

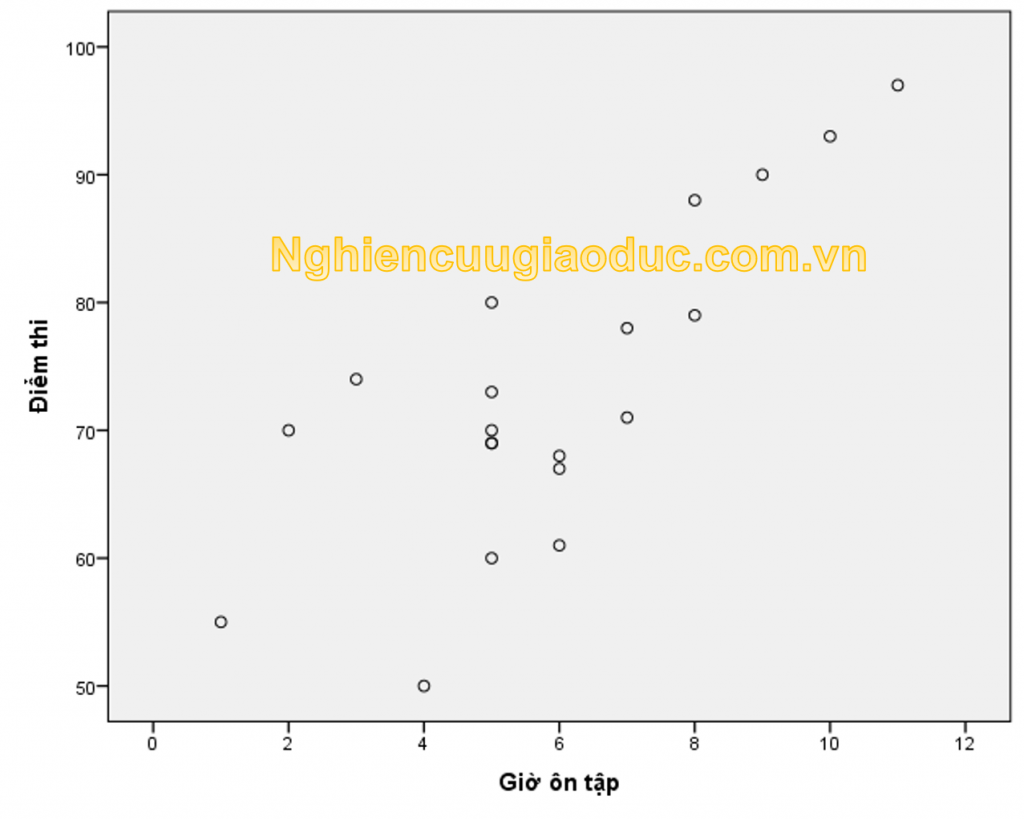
Nhận xét: Biểu đồ phân tán giữa điểm kiểm tra và điểm sửa đổi gợi ý xu hướng gần đúng tuyến tính, nhưng kích thước mẫu nhỏ để quan sát rõ ràng một đường tuyến tính. trong thực tế, chúng tôi cần kích thước mẫu lớn hơn, ít nhất là n & gt; 30. Biểu đồ này cũng cho thấy một ngoại lệ rất rõ ràng (điểm gần giá trị 4 trên trục hoành).

– bước 2: Khi biểu đồ phân tán dự đoán mối quan hệ tuyến tính, chúng tôi thực hiện phân tích tương quan r của Pearson. nhấp vào phân tích-> bản đồ – & gt; lưỡng biến…

– bước 3: trong hộp thoại tương quan hai biến , chúng tôi di chuyển các biến có mối tương quan sẽ được kiểm tra trong hộp biến . hãy nhớ chọn hộp pearson trong vùng hệ số tương quan . sau đó nhấp vào ok để chạy kết quả.

phân tích kết quả:

Bảng

về mối tương quan hiển thị hệ số tương quan Pearson r, giá trị p quan trọng của nó và kích thước mẫu được tính toán. Trong ví dụ này, chúng ta có thể thấy rằng hệ số tương quan Pearson, r, là 0,78 và có ý nghĩa thống kê (p = 0,000).

Xem thêm: Cách làm bánh bông lan bằng nồi cơm điện đơn giản mà ngon

Chúng tôi có thể báo cáo rằng mối tương quan Pearson đã được chạy để xác định mối quan hệ tuyến tính giữa điểm cuối cùng của các bài kiểm tra viết bằng toán giải thích và số giờ ôn tập của học sinh. Kết quả cho thấy có mối tương quan thuận giữa điểm của bài thi viết cuối kỳ môn Toán có lời giải và số giờ ôn tập của học sinh (r = 0,780, n = 20, p = 0,000).

– bước 4: kiểm tra tầm quan trọng của hệ số tương quan r

Khi mối tương quan đã được tính toán, nhà nghiên cứu có thể muốn biết khả năng xảy ra mối tương quan thu được này, tức là nó có phải là một sự may rủi hay nó đại diện cho một mối tương quan dân số đáng kể?

đối với điều này, r được chuyển đổi và xác suất của công cụ ước tính này dựa trên phân phối lấy mẫu của thống kê t (t-Statistics). do đó, tầm quan trọng của hệ số tương quan Pearson thu được được đánh giá bằng cách sử dụng phân phối t (t-Distribution) với n – 2 bậc tự do có độ lớn (df) và được đưa ra bởi phương trình sau :

Giả thuyết rỗng được kiểm định dưới dạng hai biến độc lập, tức là không có mối quan hệ tuyến tính giữa chúng, h0: ρ = 0. Giả thuyết thay thế là, h1: ρ ≠ 0.

Để trả lời câu hỏi, có mối tương quan đáng kể, ở mức 5%, giữa điểm kiểm tra viết cuối kỳ môn toán giải thích và số giờ ôn tập mà học sinh dành không? t sẽ được tính như sau:

Xem Thêm : Nồng độ mol là gì? Công thức tính số mol, nồng độ mol?

tra cứu bảng giá trị t tới hạn để nhận giá trị 2.101 . thống kê thử nghiệm t vượt quá giá trị tới hạn này (5,433> 2,101) và do đó giả thuyết vô hiệu bị bác bỏ. chúng tôi kết luận rằng mối tương quan là đáng kể ở mức 5%.

– bước 5: kiểm tra khoảng tin cậy của hệ số tương quan r

khoảng tin cậy

dựa trên sự chuyển đổi thống kê r thành thống kê Fisher z . điều này không giống với độ lệch z (độ lệch z) từ phân phối chuẩn (đôi khi được gọi là điểm số z). Để diễn giải khoảng tin cậy, Điểm z Fisher phải được chuyển đổi trở lại số liệu tương quan. fish’s z được phân loại là:

Xem thêm: TOP 3 cách nấu nước dashi thơm ngon, bổ dưỡng cho bé | VinID

Khoảng tin cậy (95%) cho mối tương quan biến thiên giữa điểm cuối cùng của bài kiểm tra toán có lời giải và số giờ ôn tập của học sinh được tính bằng công thức:

công thức chuyển đổi fish’s z được định nghĩa là:

áp dụng các công thức ví dụ (với r = 0,78), chúng tôi có:

khoảng tin cậy (95%):

= 0,57 đến 1,52

Giờ đây, những giá trị này sẽ được chuyển đổi trở lại số liệu ban đầu.

Nhận xét: Chúng tôi có thể kết luận rằng chúng tôi chắc chắn 95% rằng mối tương quan dân số là dương và nằm trong khoảng từ 0,515 đến 0,909 . khoảng tin cậy này không bao gồm giá trị 0 , cho thấy mối tương quan có ý nghĩa thống kê ở mức 5%.

tài liệu tham khảo

1. coolicano, h. (2018). Phương pháp nghiên cứu và thống kê trong tâm lý học. routledge.
2. hanneman, r. a., kposowa, a. j., & amp; bí ẩn, m. d. (2012). thống kê cơ bản cho nghiên cứu xã hội (quyển 38). John Wiley & amp; con trai.
3. jackson, s. tôi (2015). Phương pháp nghiên cứu và thống kê: Phương pháp tiếp cận tư duy phản biện. học tập liên tục.
4. mcqueen, r. a., & amp; knussen, c. (Năm 2006). Giới thiệu về phương pháp nghiên cứu và thống kê trong tâm lý học. giáo dục pearson.
5. nghiên cứu sinh, tôi. (Năm 2006). Phân tích thống kê cho các nhà nghiên cứu trong giáo dục và tâm lý học: công cụ cho các nhà nghiên cứu trong giáo dục và tâm lý học. routledge.
6. wagner iii, w. tôi. (2019). Sử dụng Thống kê SPSS® của IBM cho các Phương pháp Nghiên cứu và Thống kê Khoa học Xã hội. bài đăng của hiền triết.