Diện tích tam giác: Công thức tổng hợp chương trình lớp 5, 10, 12

1. công thức tính diện tích tam giác vuông là gì?

Để biết công thức tính diện tích tam giác vuông, chúng ta cần xác định loại tam giác này. Tam giác vuông là tam giác có góc vuông 90 độ. Trong loại tam giác này, cạnh huyền (cạnh đối diện với góc vuông) là cạnh dài nhất. và hai cạnh còn lại sẽ vuông góc với nhau.

1.1. công thức tính diện tích tam giác vuông truyền thống

Tam giác vuông cũng có thể tính diện tích bằng cách nhân chiều cao với cơ sở và chia cho 2 như bình thường. Điểm khác biệt với loại tam giác này là học sinh không cần tính chiều cao của tam giác. lý do: chiều cao của tam giác sẽ tương ứng với một cạnh của góc vuông. và chiều dài sẽ là cạnh của góc vuông còn lại.

thì công thức tính diện tích sẽ là: s = (a x b) / 2. trong đó a, b là độ dài hai cạnh của góc vuông.

Bài tập mẫu: tìm diện tích của một tam giác vuông có các cạnh lần lượt là 3 cm và 4 cm. Với bài tập này, học sinh áp dụng ngay công thức trên sẽ có: s = (3 x 4) / 2 = 6 cm2.

lưu ý : diện tích luôn là đơn vị hình vuông (m2, cm2, mm2…). học sinh trong câu trả lời cần kiểm tra kỹ, nếu viết đơn vị bình thường sẽ sai.

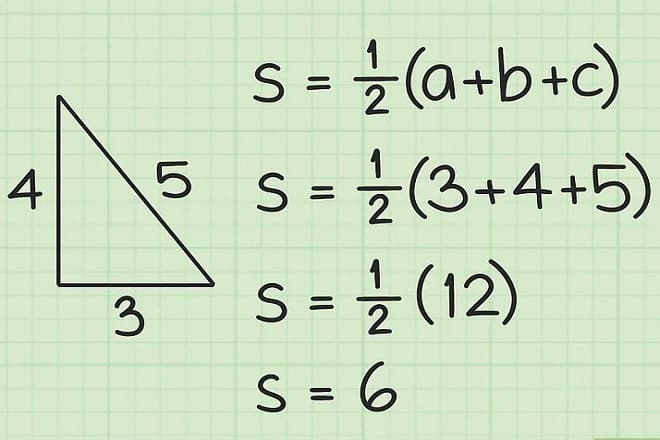
1.2. Cách tính diện tích khi biết chiều dài cạnh huyền

Với bài toán biết độ dài hai cạnh góc vuông, chúng ta có thể dễ dàng tính được diện tích. nhưng thường bài toán sẽ khó hơn khi chỉ cho độ dài một cạnh góc vuông và độ dài cạnh huyền. Từ đây để tính diện tích tam giác vuông ta cần thêm một số bước như sau:

• Tìm độ dài cạnh còn lại của góc vuông bằng Định lý Pitago. định lý này nói rằng bình phương của cạnh huyền bằng tổng bình phương của hai cạnh còn lại. vì vậy nếu chúng ta biết cạnh huyền và một cạnh của góc vuông, chúng ta có thể tính được cạnh còn lại.
• nếu chúng ta gọi cạnh huyền thì hai cạnh của góc vuông là b và c. ta sẽ có công thức: a 2 = b 2 + c 2. chẳng hạn cạnh huyền dài 5 cm, cạnh vuông góc là 4 cm. thì áp dụng công thức trước ta sẽ có: 5 2 = 4 2 + c 2. Suy ra: 25 = 16 + c 2. Từ đây ta có thể tính được cạnh của góc vuông còn lại: 3 cm.
• Bước cuối cùng là áp dụng công thức tính thông thường: s = (3 x 4) / 2 = 6 cm2.

2. cách nhanh hơn để tính diện tích tam giác đều

Xem thêm: Tỉ khối của chất khí: công thức và các dạng bài tập hay gặp

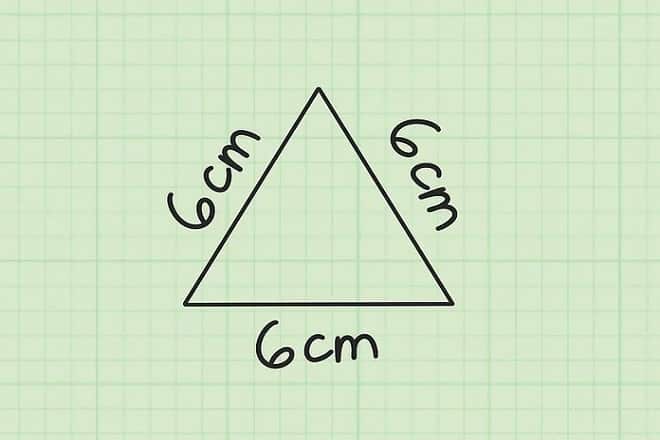
tam giác đều là một trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là cả ba góc đều bằng nhau và bằng 60 độ.

2.1. công thức tính diện tích tam giác đều lớp 5

Xem Thêm : Thực Đơn Keto Giảm Cân Cấp Tốc Trong 7 – 28 Ngày An Toàn & Siêu Ngon

Một tam giác đều tương tự như một tam giác bình thường. có nghĩa là, có một cách để tính diện tích là tích của chiều cao và đường viền dưới rồi chia cho 2. Vì vậy, đối với bài toán nói rằng hai dữ liệu là chiều cao và độ dài của đường viền dưới cùng, chúng ta áp dụng công thức s = (a x h) / 2.

trong đó s là diện tích, a là độ dài của đáy của tam giác đều và h là chiều cao (đường từ trên xuống dưới). Ví dụ, bài toán yêu cầu tìm diện tích khi độ dài cạnh của hình tam giác là 6 cm và chiều cao là 10 cm. áp dụng công thức trước, chúng ta sẽ có s = (6 x 10) / 2 = 30 cm2.

2.2. Cách tính diện tích khi chỉ biết một cạnh

Thông thường, bài toán sẽ không cho học sinh biết chiều cao của một tam giác đều. Lúc này, để tính diện tích, học sinh có thể áp dụng ngay công thức: s = (a 2) x √3 / 4. Trong đó a là độ dài cạnh của tam giác đều bình phương và nhân với √3 / 4 bằng 1732.

Ví dụ, tìm diện tích của một tam giác đều khi cạnh đó là 6 cm. Áp dụng công thức ở trên, ta sẽ có: s = 6 2 x √3 / 4 = 15,59 cm2.

Lưu ý : Với cách này, học sinh nên sử dụng hàm căn bậc hai của máy tính để có kết quả chính xác hơn. nếu không, học sinh có thể sử dụng kết quả làm tròn của √3 / 4 là 1.732. kết quả luôn được viết theo đơn vị bình phương và phải được làm tròn đến chữ số thập phân thứ hai.

3. làm thế nào để bạn tính diện tích của một tam giác cân?

Xem thêm: 7 công thức nước ép cải kale giúp da sáng dáng xinh

Tam giác cân là một loại tam giác trong đó hai cạnh và hai góc bằng nhau. trong đó cách tính diện tích tương tự như cách tính tam giác thường, chỉ biết chiều cao của tam giác và cạnh đáy.

3.1. tính diện tích khi biết chiều dài của đáy và chiều cao

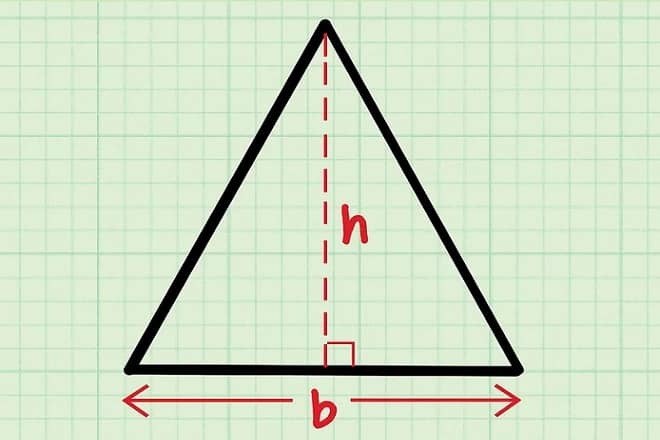
diện tích của một tam giác cân sẽ bằng tích của chiều cao nhân với cơ sở của nó chia cho 2. Công thức tổng quát sẽ là s = ​​(a x h) / 2. trong đó a là độ dài của đáy của tam giác cân, h Là chiều cao. do đó, nếu bài toán cho chúng ta biết hai dữ liệu trước đó, chúng ta có thể dễ dàng tính diện tích theo phương pháp thông thường.

Ví dụ, tìm diện tích của một tam giác cân khi chiều dài cơ sở là 6 cm và chiều cao là 7 cm. áp dụng công thức trước, chúng ta sẽ có s = (6 x 7) / 2 = 21 cm2.

3.2. Công thức tính diện tích tam giác cân theo định lý Pytago

Thông thường bài toán sẽ không đưa ra chiều cao và đường viền dưới để chúng ta có thể tính diện tích một cách dễ dàng. thay vào đó, chúng ta cần tìm cạnh cơ sở và chiều cao của tam giác cân. học sinh nhớ rằng cạnh đáy của tam giác cân là cạnh không bằng hai cạnh còn lại (tam giác cân có 2 cạnh bằng nhau).

Xem Thêm : Định luật Hooke (húc): nội dung, công thức và ứng dụng – Chia sẻ kiến thức mỗi ngày

chẳng hạn, nếu một tam giác cân có các cạnh là 5 cm, 5 cm và 6 cm. bây giờ cạnh dài 6 cm là cạnh cơ sở. các bước tiếp theo như sau:

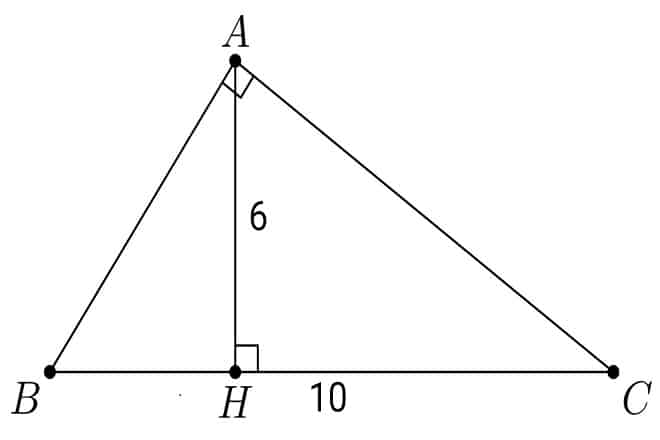
• tính chiều cao: kẻ một đoạn thẳng từ đỉnh của tam giác cân đến trung điểm của đáy. lưu ý rằng đường thẳng này vuông góc với cạnh cơ sở (chia đôi cạnh cơ sở) và là chiều cao của tam giác cân.
• lúc này, chúng ta sẽ thấy rằng tam giác cân chia thành 2 tam giác vuông nhờ đó chúng ta có thể tìm được chiều cao thông qua định lý Pitago nổi tiếng. Cụ thể, chúng ta có cạnh vuông góc 3 cm (vì chiều cao chia đôi mặt đáy) và cạnh huyền là 5 cm. áp dụng định lý Pitago: a 2 = b 2 + c 2 ta có 5 2 = 3 2 + c 2. suy ra: 25 = 9 + c 2. từ đây chúng ta có thể tính được góc vuông còn lại (cũng là chiều cao) là: 4 cm.
• áp dụng công thức thông thường cho diện tích s = (a x h) / 2. bây giờ chúng ta có độ dài cơ sở là 6, h chiều cao của tam giác cân là 4. nên diện tích sẽ là s = ​​(6 x 4) / 2 = 12 cm2.

3.3. tính diện tích hình bình hành

Có một điều khá thú vị trong hình học là tam giác cân và hình bình hành có mối quan hệ “khá chặt chẽ” với nhau. Cụ thể, nếu ta cắt đôi hình bình hành theo đường xiên thì sẽ tạo thành 2 tam giác cân có diện tích bằng nhau. Tương tự, nếu bạn có hai tam giác cân giống nhau, bạn có thể kết hợp chúng để tạo thành một hình bình hành. nghĩa là diện tích của bất kỳ tam giác cân nào sẽ có công thức s = 1/2 (a x h) (a là cơ sở, h là chiều cao), chính xác là một nửa diện tích của hình bình hành tương ứng.

Xem thêm: QUY TRÌNH TẠO RA 1001 CÔNG THỨC NHUỘM TÓC ĐẸP, BỀN MÀU 

sau đó, với công thức trên, chúng ta tính diện tích hình bình hành và chia nó cho 2 để được diện tích tam giác cân. Tất nhiên, với cách này chúng ta cũng cần tìm chiều cao theo định lý Pitago mà yeutre.vn đã hướng dẫn ở phần 3.2. Cụ thể, chúng tôi đã tính toán rằng chiều cao của đỉnh là 4 cm, sau đó áp dụng công thức này, chúng tôi sẽ có s = 1/2 (6 x 4) = 12 cm2.

4. cách nhanh nhất để tính diện tích tam giác vuông cân

Tam giác vuông cân là một loại tam giác có hai cạnh bằng nhau và một góc bằng 90 độ. đây cũng là dạng tam giác có cách tính diện tích đơn giản nhất.

• công thức cụ thể là s = ​​1/2 (a x h). hoặc s = 1/2 đến 2
• trong đó a là cạnh của đáy và cũng là chiều cao vì hai cạnh bằng nhau trong một tam giác vuông cân.

lưu ý : một số vấn đề sẽ không chỉ ra cạnh của đế hoặc chiều cao. thay vào đó, chúng chỉ cho biết độ dài của cạnh huyền. Ở phần này, học sinh nhớ áp dụng Định lý Pitago để tìm độ dài của đáy và chiều cao (có giá trị bằng nhau).

5. Những điều cần biết khi tính diện tích hình tam giác

Như chúng tôi đã đề cập, cách tính diện tích của một tam giác là nhân cơ sở với chiều cao và chia nó cho hai. tuy nhiên, đối với môn Toán, đặc biệt là trong đề thi hiện nay sẽ không có hai phần thông tin là cạnh đáy và chiều cao. thay vào đó, học sinh phải tìm hai phần thông tin này thông qua một số thông tin đã cho. Dưới đây là các bước chi tiết để tìm diện tích tam giác đều mà các em học sinh cần biết.

5.1. tìm đáy và chiều cao của tam giác

• đáy là một cạnh của tam giác và chiều cao là đoạn thẳng nối đỉnh cao nhất với đáy của tam giác đó.
• thông thường bài toán sẽ đưa ra cơ sở hoặc Chiều cao. và tùy theo dạng tam giác, học sinh sẽ tìm được 2 dữ kiện này. với chiều cao, học sinh cần kẻ một đường thẳng vuông góc với mặt đối diện từ trên xuống dưới. sau đó áp dụng định lý Pitago được trình bày chi tiết ở trên để tính chiều cao.

5.2. áp dụng cho công thức cho diện tích

• Công thức cho diện tích của hình này là s = ​​(a x h) / 2. trong đó s là diện tích, a là chiều dài của đáy và h là chiều cao của tam giác.
• học sinh tìm đáy và chiều cao, sau đó áp dụng công thức trên. nhanh chóng tạo hai giá trị chiều sâu và chiều cao, sau đó chia cho 2 để tìm diện tích cần tìm.
• lưu ý rằng diện tích luôn là đơn vị hình vuông (m2, cm2…).

>

Bên cạnh các cách tính diện tích hình tam giác hợp theo sgk ngữ văn lớp 5, lớp 10 và lớp 12, còn có các cách khác để áp dụng công thức tính diệc. hoặc một cách khác là sử dụng hàm lượng giác. tuy nhiên hai cách này khá khó và nhìn chung chỉ áp dụng cho học sinh cấp 3. Ngoài công thức toán trên, các em có thể tham khảo thêm cách tính diện tích hình tròn mà chúng tôi đã giới thiệu. Chúc mọi người nắm vững kiến ​​thức và làm bài tốt.

ducloc