Hình học 12 Bài 2: Phương trình mặt phẳng

a) biểu hiện phối hợp của sản phẩm được nhắm mục tiêu

cho hai vectơ ( vec {a} = (x_1; y_1; z_1) ) và ( vec {b} = (x_2; y_2; z_2) ), vectơ ( overrightarrow n = left [{ overrightarrow a; overrightarrow b} right] ) được gọi là tích có hướng của hai vectơ ( overrightarrow a ) và ( overrightarrow b ) được định nghĩa như sau:

( left [{ vec a, vec b} right] = left ({ left | { begin {array} {* {20} {c}} {{y_1} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} {z_1}} \ {{y_2} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} { z_2}} end {matrix}} right |; left | { begin {matrix} {* {20} {c}} {{z_1} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} {x_1}} \ {{z_2} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} {x_2}} end {array}} right | ; left | { begin {array} {* {20} {c}} {{x_1} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} {y_1}} \ {{x_2} ; { mkern 1mu} ; { mkern 1mu} ; { mkern 1mu} {y_2}} end {matrix}} right |} right) = ({y_1} {z_2} – {y_2} {z_1}; {z_1} {x_2} – {z_2} {x_1}; {x_1} {y_2} – {x_2} {y_1}) )

b) thuộc tính

vectơ ( overrightarrow n ) vuông góc với cả vectơ ( overrightarrow a ) và ( overrightarrow b. )

c) ứng dụng của sản phẩm được nhắm mục tiêu

• kiểm tra tính đồng phẳng của vectơ:
  • ( vec {a}, vec {b}, vec {c} ) không phải là đồng phẳng nếu và chỉ khi ( left [ vec {a}, vec {b} right] vec {c} neq 0. ) suy ra rằng 4 điểm a, b, c, d không đồng phẳng nếu và chỉ khi ( left [ overrightarrow { ab}, overrightarrow {ac} right] overrightarrow {ad} neq 0 ).
  • ( vec {a}, vec {b}, vec {c} ) là đồng phẳng nếu và chỉ khi ( left [ vec {a}, vec {b} right] vec {c} = 0 ). suy ra rằng a, b, c, d là đồng phẳng nếu và chỉ khi ( left [ overrightarrow {ab}; overrightarrow {ac} right] overrightarrow {ad} = 0 ).
  • Diện tích hình bình hành abcd: (s_ {abcd} = left | left [ overrightarrow {ab}; overrightarrow {ac} right] right | ).
  • diện tích tam giác ( delta abc ): (s _ { delta abc} = frac {1} {2} left | left [ overrightarrow {ab}; overrightarrow {ac} right] right | ).

  a) vectơ pháp tuyến phẳng

  cho căn hộ (p). nếu vectơ ( vec n ) khác với ( vec 0 ) có giá trị vuông góc với (p) thì ( vec n ) được gọi là vectơ pháp tuyến của (p).

  b) phương trình tổng quát của mặt phẳng

  Phương trình tổng quát của mặt phẳng có dạng: (Ax+By+Cz+D=0, ,, A^2+B^2+C^2neq 0)). Với (overrightarrow{n}=(A;B;C)) là Vectơ pháp tuyến (VTPT).

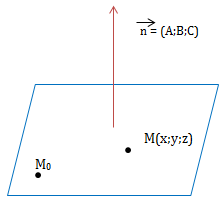
  c) viết phương trình của một mặt phẳng khi biết vectơ pháp tuyến và một điểm trên mặt phẳng đó

  Xem thêm: Công Thức Tính Vận Tốc Truyền Sóng V, Bước Sóng Λ, Chu Kỳ T, Tính Vận Tốc Truyền Sóng

  mặt phẳng (p) đi qua điểm ({{m_0} ({x_0}; {y_0}; {z_0})} ), thu được vectơ ({ vec n = (a; b; c )} ) làm vtpt với phương trình tổng quát:

  Xem Thêm : Công Thức Tính Số Vòng Dây Quấn Motor 1 Pha, Cách Tính Số Vòng Dây Motor

  (a (x-x_0) + b (y-y_0) + c (z-z_0) = 0 )

  d) phương trình của mặt phẳng theo giao tuyến

  mặt phẳng (p) đi qua a (a, 0,0), b (0, b, 0), c (0,0, c) có phương trình tổng quát là: ( frac {x} {a } + frac {y} {b} + frac {z} {c} = 1 ).

  e) một số cách xác định vectơ pháp tuyến của mặt phẳng

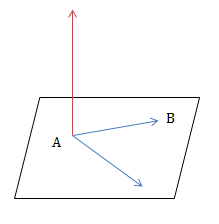
  • gọi ( vec n ) vtpt của mặt phẳng (p), giả sử sự tồn tại của ( vec u_1 ) và ( vec u_2 ) sao cho ( left. begin {matrix} vec {n} perp overrightarrow {u_1} \ vec {n} perp overrightarrow {u_2} end {matrix} right } ) rồi ( vec {n} = left [ overrightarrow {u_1}; overrightarrow {u_2} right] ) là vtpt của mặt phẳng (p).
  • mặt phẳng (abc) có vtpt ( vec {n)} = left [ overrightarrow {ab}; overrightarrow {ac} right] ).

  

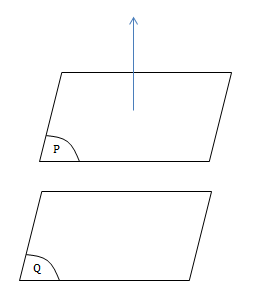
  • mặt phẳng (p) song song với mặt phẳng (q):
    • được gọi là: ( overrightarrow {n} _p ) là vtpt của (p), ( overrightarrow { n} _q ) là vtpt của (q) nên: ( overrightarrow {n} _p = overrightarrow {n} _q. )

    

    • đối với đường thẳng ab và mặt phẳng (p): ( Big lbrack begin {matrix} ab subset (p) \ ab // (p) end {matrix} ) thì ( vec {n_p} perp overrightarrow {ab}. )
    • if ((p) perp (q) ) then ( overrightarrow {n} _p perp overrightarrow {n} _q ).

    Xem thêm: Lý thuyết. Dòng điện không đổi. Nguồn điện

    cho hai mặt phẳng (( alpha _1) a_1x + b_1y + c_1z + d_1 = 0 ) tồn tại một vtpt ( vec {n_1} = (a_1; b_1; c_1) ) và (( alpha _2) a_2x + b_2y + c_2z + d_2 = 0 ) có vtpt ( vec {n_2} = (a_2; b_2; c_2) ).

    thì vị trí tương đối giữa (( alpha_1) ) và (( alpha_2) ) được xác định như sau:

    • (( alpha _1) // ( alpha _2) ) nếu và chỉ khi ( left { begin {matrix} vec {n_1} = k. vec {n_2} \ d_1 neq d_2 end {array} right. ).

    if (a_2, b_2, c_2, d_2 neq 0 ): (( alpha _1) // ( alpha _2) leftrightarrow frac {a_1} {a_2} = frac {b_1} { b_2} = frac {c_1} {c_2} neq frac {d_1} {d_2} ).

    • (( alpha _1) equiv ( alpha _2) ) nếu và chỉ khi ( left { begin {matrix} vec {n_1} = k. vec {n_2} \ d_1 = k.d_2 end {array} right. ).

    Xem Thêm : Công thức tính chiều dài, chiều rộng hình chữ nhật và bài tập áp dụng

    if (a_2, b_2, c_2, d_2 neq 0 ) then (( alpha _1) equiv ( alpha _2) leftrightarrow frac {a_1} {a_2} = frac {b_1} { b_2} = frac {c_1} {c_2} = frac {d_1} {d_2} ).

    • (( alpha _1), ( alpha _2) ) cắt nhau nếu và chỉ khi ( vec {n_1} neq k. vec {n_2} ).

    if (a_2, b_2, c_2 neq 0 ) then (( alpha _1), ( alpha _2) ) giao nhau ( leftrightarrow expand lbrack begin {matrix} frac { a_1} {a_2} neq frac {b_1} {b_2} \ frac {a_1} {a_2} neq frac {c_1} {c_2} \ frac {b_1} {b_2} neq frac { c_1} {c_2} end {array} ).

    Xem thêm: Công Thức Viết Phương Trình Tiếp Tuyến Của đồ Thị Hàm Số (C) Y F(x) Song Song Với đường Thẳng D: Y Ax B | Lessonopoly

    cho mặt phẳng (p): (ax + by + cz + d = 0 (a ^ 2 + b ^ 2 + c ^ 2 neq 0) ) và điểm (m (x_0, y_0), z_0) ). khoảng cách từ m đến (p) được xác định theo công thức: (d (m; (p)) = frac { left | ax_0 + ay_0 + az_0 + d right |} { sqrt {a ^ 2 + b ^ 2 + c ^ 2}} ).

    cho hai mặt phẳng ((p) ; {a_1} x + {b_1} y + {c_1} z + {d_1} = 0 ) và ((q) ; {a_2} x + {b_2 } y + {c_2} z + {d_2} = 0 ) có vtpt tương ứng:

    ( vec {n} _p = (a_1; b_1; c_1) ) và ( vec {n} _q = (a_2; b_2; c_2) ), sau đó:

    (cos widehat {(p, q)} = left | {cos ({{ vec n} _p}; {{ vec n} _q})} right | = frac {{ left | {{{ vec n} _p}. {{ vec n} _q}} right |}} {{ left | {{{ vec n} _p}} right | left | {{ { vec n} _q}} right |}} ) (= frac { left | a_1b_2 + b_1b_2 + c_1c_2 right |} { sqrt {a ^ 2_1 + b_1 ^ 2 + c ^ 2_1}. sqrt {a ^ 2_2 + b_2 ^ 2 + c ^ 2_2}} )

    chú ý:

    • (0 ^ 0 leq ( widehat {p, q}) leq 90 ^ 0 ).
    • ((p) perp (q) leftrightarrow vec {n} _p. vec {n} _q ) ( leftrightarrow a_1a_2 + b_1b_2 + c_1c_2 = 0 ).