Modun số phức và các tính chất liên quan

Môđun của một số phức là gì? Nếu bạn cần hiểu môđun và các tính chất liên quan của số phức. Để đạt điểm cao trong kỳ thi, hãy theo dõi các bài viết dưới đây. Tôi sẽ cố gắng trình bày và giải thích theo cách rõ ràng nhất có thể và cung cấp cho bạn những hình ảnh minh họa dễ hiểu. Giữ nguyên!

Tôi. Mô-đun số nhiều

Tôi cảm thấy thú vị khi tôi dạy sinh viên khái niệm về mô-đun. Hầu hết các bạn chưa học qua đều ngạc nhiên với từ “modular”. Có lẽ bởi vì nó là một phiên âm tiếng Anh.

modun (tiếng Anh: modulus hoặc giá trị tuyệt đối) của số phức z = a + bi (a, b∈r) là căn bậc hai số học (hoặc căn bậc hai không âm) của a² + b². Ví dụ, 3 + 4i có 3² + 4² = 25, do đó mô-đun của 3 + 4i là 5. Chúng ta cũng ký hiệu môđun của z = a + bi là | z | hoặc | a + bi |. Lưu ý rằng số thực cũng là số phức. Ta cũng dễ dàng nhận thấy rằng giá trị tuyệt đối của một số thực cũng chính là môđun của số thực đó. Do đó đôi khi chúng ta gọi môđun của một số phức là giá trị tuyệt đối của số phức.

Ví dụ:

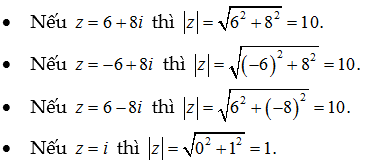
Xem thêm: Hướng dẫn chi tiết cách tính cân nặng lý tưởng theo chỉ số BMI – Thế Giới Điện Giải

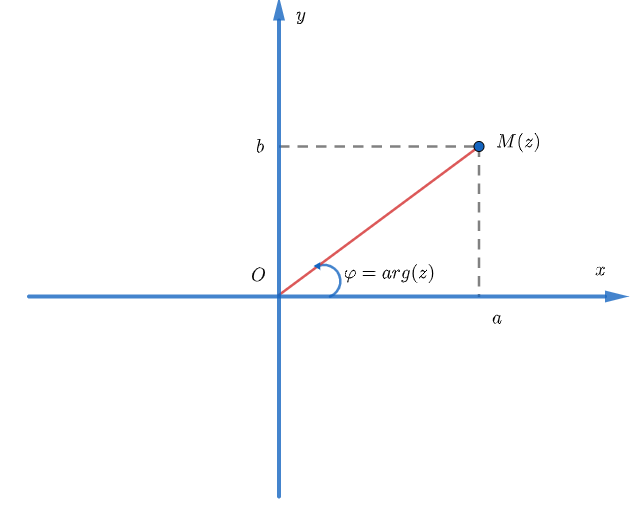
Về mặt hình học, mọi số phức z = a + bi (a, b∈r) được biểu diễn bởi một điểm m (z) = (a; b) trên mặt phẳng Oxy và ngược lại. Khi đó môđun của z được biểu diễn bằng độ dài đoạn thẳng om (z). Rõ ràng, môđun của z là một số thực không âm, chỉ bằng 0 khi z = 0.

Hai. Tính mô đun của số nhiều

Xem Thêm : 3 cách làm trứng gà nướng thơm ngon, không bị trào, bể | VinID

Sử dụng môđun của số phức, chúng ta có thể dễ dàng chứng minh các tính chất sau:

(i) Hai số phức đối nhau có cùng môđun. Đó là | z | = | -z |.

(ii) Hai số phức liên hợp có cùng môđun. Đó là | a + bi | = | a-bi |.

(iii) Môđun của z bằng 0 nếu và chỉ khi z = 0.

Xem thêm: Công thức tính điểm thi tốt nghiệp THPT 2022 chuẩn nhất – META.vn

(iv) Tích của hai số phức liên hợp bằng bình phương mô đun của chúng

(v) mô-đun của sản phẩm là sản phẩm của mô-đun

(vi) Môđun của một thương số bằng thương số của một môđun

Bộ đề kiểm tra trực tuyến với lời giải chi tiết: số phức

Ba. Vô thức theo mô-đun

Xem Thêm : Mẫu công văn giải trình chậm chuyển Đảng chính thức

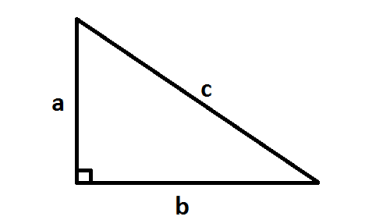
Vì môđun của một số phức là độ dài của một đoạn thẳng trong mặt phẳng. Do đó, từ các bất đẳng thức tam giác, chúng ta có thể suy ra các bất đẳng thức mô đun tương tự.

• Tổng hai cạnh của một tam giác luôn lớn hơn cạnh thứ ba. Khi đó, chúng ta có bất bình đẳng:

Dấu bằng xuất hiện trong

Xem thêm: Cách ướp thịt heo nướng ngon đúng chuẩn nhà hàng

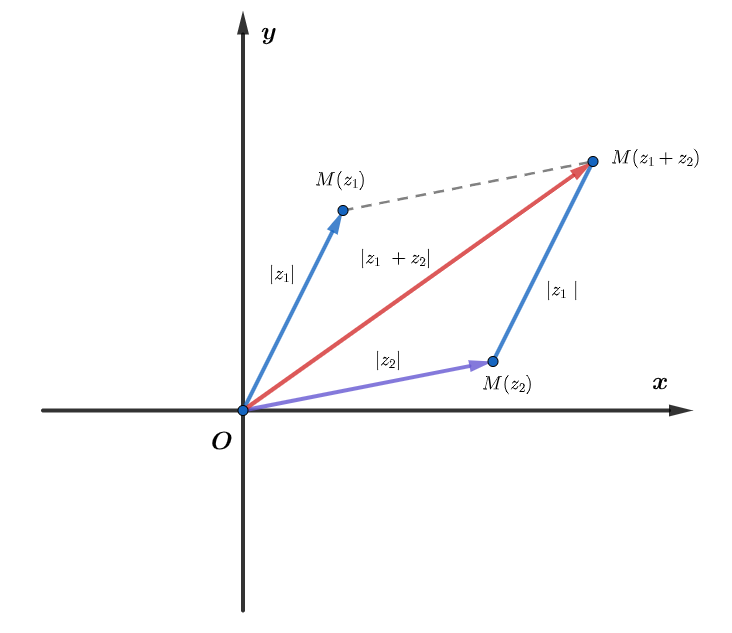
Cũng từ bất đẳng thức tam giác trên, chúng ta có thể suy ra:

Dấu bằng xuất hiện trong

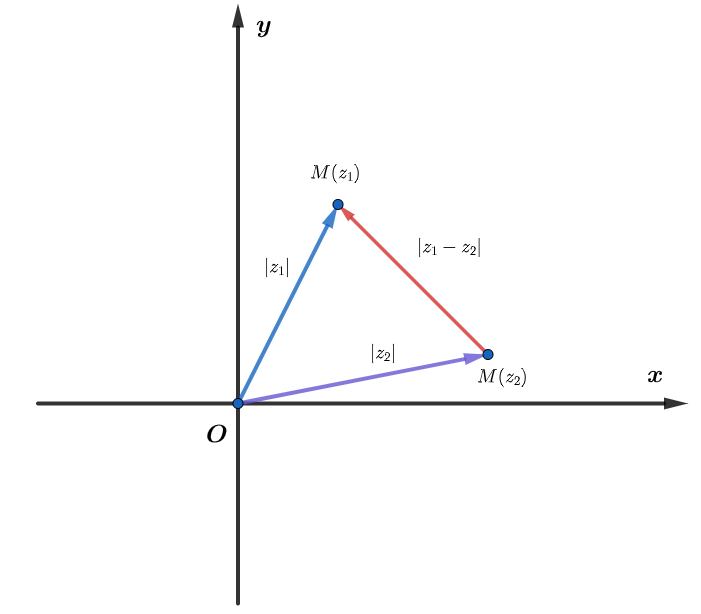
• Đúng như bất đẳng thức tam giác: “Hiệu giữa hai cạnh của tam giác luôn nhỏ hơn cạnh thứ ba, và ta có thể suy ra bất đẳng thức sau:

Trên đây là định nghĩa về môđun phức mà toanthaydinh.com gửi đến các bạn, một số tính chất chung của môđun phức và một số bất đẳng thức môđun thường gặp. Nếu bài viết được nhiều người quan tâm, tôi sẽ tiếp tục viết về ứng dụng của tính chất môđun phức vào bài toán cực trị của số phức. Cảm ơn đã xem!

Xem Thêm: Hoàn thành các bài tập về Số nhiều

• Cách quay số nhiều trên casio 580 vnx

  Dạng tam giác và ứng dụng của số phức

  Phép chia phức tạp hoạt động như thế nào?

  Tìm số phức z thỏa mãn các điều kiện cho trước

  Làm thế nào để tìm một tập hợp các điểm biểu diễn các số phức?