✅ Công thức bất đẳng thức ⭐️⭐️⭐️⭐️⭐

bất bình đẳng và ứng dụng

i. khái niệm cơ bản về bất bình đẳng

1.1 số thực dương, số thực âm

nếu a là một số thực dương, chúng tôi ký hiệu là a> 0

nếu a là số thực âm, chúng tôi ký hiệu & lt; 0

nếu a là một số thực dương hoặc a = 0, chúng ta nói rằng a là một số thực không âm, được ký hiệu là a≥0a≥0

nếu a là một số thực âm hoặc a = 0, chúng ta nói rằng a là một số thực không dương, được ký hiệu là a≤0a≤0

lưu ý: đối với hai số thực a và b, chỉ có một trong ba khả năng sau:

a & gt; b hoặc a

phủ định của mệnh đề a & gt; 0 là a≤0a≤0

sự phủ định của một mệnh đề

Bất đẳng thức có được từ hằng đẳng thức dạng (a−b)2≥0

Bất đẳng thức AM – GM (Sách giáo khoa việt nam gọi là bất đẳng thức Côsi)

Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa việt nam gọi là bất đẳng thức Bunhiacopsky)

Bất đẳng thức Cauchy – Schwarz dạng phân thức

Bất đẳng thức Mincopski (bất đẳng thức véctơ)

Bài 1. Cho các số thực dương a, b, c thỏa mãn a2 + b2 + c2 = 3.

kiểm tra rằng:

Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.

xem xét sự bất bình đẳng

1. khái niệm bất bình đẳng

– các mệnh đề có dạng “a & lt; b” hoặc “a & gt; b” được gọi là bất đẳng thức.

2. bất bình đẳng hệ quả và bất bình đẳng tương đương

– nếu phát biểu “a & lt; b ⇒ c & lt; d” là đúng, thì chúng ta nói rằng bất đẳng thức c & lt; d là bất đẳng thức hệ quả của a & lt; b và chúng ta cũng viết a & lt; b ⇒ c & lt; d.

– nếu bất đẳng thức a & lt; b tiếp theo từ bất đẳng thức c & lt; d và ngược lại, thì chúng ta nói rằng hai bất đẳng thức là tương đương và viết a & lt; b ⇔ c & lt; d.

3. các tính chất của bất đẳng thức

° cộng cả hai vế của bất đẳng thức bằng một số:

a & lt; b ⇔ a + c & lt; b + c

° Nhân cả hai vế của bất đẳng thức với một số:

– với c & gt; 0: a & lt; b ⇔ ac & lt; ac

– với c & lt; 0: a & lt; b ⇔ ac & gt; ac

° cộng với hai bất phương trình cùng phương

a & lt; b và c & lt; d ⇒ a + c & lt; b + d

° bởi hai bất phương trình cùng phương

– với a & gt; 0, c & gt; 0: a & lt; b và c & lt; d ⇒ ac & lt; bd

Xem thêm: Áp suất chất lỏng & Công thức tính áp suất chất lỏng

° nâng cả hai mặt của sự bất bình đẳng lên thành sức mạnh

– với n ∈ n *: a & lt; b ⇔ a2n + 1 & lt; b2n + 1

– với n ∈ n * và a & gt; 0: a & lt; b ⇔ a2n & lt; b2n

° gốc ở cả hai phía của một bất bình đẳng

2. Các hệ quả của Bất đẳng thứ Cô-si

° hệ quả 1: tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

Bất đẳng thức chứa dấu trị tuyệt đối

Từ định nghĩa về giá trị tuyệt đối, chúng ta có bất đẳng thức về giá trị tuyệt đối sau đây

° | x | ≥ 0, | x | x, | x | -x

Xem Thêm : BENZENA DAN TURUNANNYA – SMA Syarif Hidayatullah Grati

° với a> 0:

| x | 0 ⇔ -a x ≤ a

| x | a ⇔ x -a hoặc x ≥ a

° | a | – | b | ≤ | a + b | | a | + | b |

bài tập về ứng dụng của bất đẳng thức

* bài 1 trang 79 sgk Đại Số 10 : giá trị nào sau đây đúng với mọi giá trị của x?

a) 8x & gt; 4x; b) 4x & gt; 8x

c) 8×2 & gt; 4×2; d) 8 + x & gt; 4 + x

* giải pháp:

– câu trả lời đúng: d) 8 + x & gt; 4 + x

– vì 8 & gt; 4 thì cho tất cả x 8+ x & gt; 4+ x (tính chất cộng cả hai vế của bdt với một số). phải khẳng định rằng d đúng với mọi giá trị của x.

+ các câu trả lời khác sai vì:

a) chúng tôi có: 8 & gt; 4 phải là 8x & gt; 4x thì x & gt; 0

– do đó chỉ đúng khi x & gt; 0 (nói cách khác, nếu x <0, thì a là sai)

b) chúng ta có: 4 & lt; 8 phải là 4x & gt; 8x thì x & lt; 0.

– vì vậy câu lệnh chỉ đúng khi x & lt; 0

c) chỉ đúng khi x 0

bài 2 trang 79 SGK Đại số 10 : cho số x & gt; 5, số nào sau đây là số nhỏ nhất?

Xem thêm: [TỔNG HỢP] 6 Cách Làm Nước Chấm Bánh Tráng Đơn Giản Nhất

a = 5 / x; b = 5 / x + 1; c = 5 / x – 1; d = x / 5.

* giải pháp:

– với bất kỳ x ≠ 0 nào, chúng ta luôn có: – 1 & lt; 0 & lt; 1. do đó,

→ Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.

* bài 3 trang 79 sgk Đại Số 10 : Gọi a, b, c là độ dài ba cạnh của một tam giác.

1) kiểm tra (b – c) 2 & lt; a2

2) từ đó sau: a2 + b2 + c2 & lt; 2 (ab + bc + ca)

* giải pháp:

1) (b-c) 2 & lt; a2

– vì a, b, c là độ dài 3 cạnh của tam giác nên tổng 2 cạnh luôn lớn hơn cạnh còn lại. ⇒ a + c & gt; b và a + b & gt; c (bất đẳng thức tam giác)

– ta có: (b – c) 2 – a2 = (b – c – a) (b – c + a)

tạo b & lt; a + c ⇒ b – a – c & lt; 0 và b + a & gt; c & aacute; c ⇒ b + a – c & gt; 0.

suy ra: (b – c – a) (b – c + a) & lt; 0 ⇔ (b – c) 2 – a2 & lt; 0 ⇔ (b – c) 2 & lt; a2

2) từ kết quả của câu 1) chúng ta có

a2 & gt; (b – c) 2

Xem Thêm : Bài 3: Trung bình và trung vị – Tìm về những giá trị căn bản

b2 & gt; (a – c) 2

c2 & gt; (a – b) 2

– cộng với vế thứ ba của bất đẳng thức trước, chúng ta có:

a2 + b2 + c2 & gt; (b – c) 2 + (c – a) 2 + (a – b) 2

⇒ a2 + b2 + c2 & gt; b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2

⇒ a2 + b2 + c2 & gt; 2 (a2 + b2 + c2) – 2 (ab + bc + ca)

⇒ a2 + b2 + c2 & lt; 2 (ab + bc + ca) (dpcm).

bài 4 trang 79 sgk Đại Số 10 : chứng minh rằng: x3 + y3 ≥ x2y + xy2, ∀x, y ≥ 0

* giải pháp:

Xem thêm: Cách lùi xe ô tô chuẩn nhất và những quy tắc &quotvàng&quot phải nhớ

với x ≥ 0; y 0 thì x + y ≥ 0

chúng ta có: x3 + y3 x2y + xy2

⇔ (x3 + y3) – (x2y + xy2) 0

⇔ (x + y) (x2 – xy + y2) – xy (x + y) ≥ 0

⇔ (x + y) (x2 – xy + y2 – xy) 0

⇔ (x + y) (x2 – 2xy + y2) 0

⇔ (x + y) (x – y) 2 ≥ 0 (luôn đúng vì x + y ≥ 0; (x – y) 2 ≥ 0)

dấu “=” xảy ra khi (x – y) 2 = 0 ⇔ x = y.

* bài 5 trang 79 SGK Đại số 10 hãy chứng minh rằng:

+ Xét 0 ≤ t < 1 ⇒ t3 < 1 ⇒ 1 – t3 > 0 ; 1 – t > 0

t8 – t5 + t2 – t + 1 = t8 + (t2 – t5) + (1 – t) = t8 + t2. (1 – t3) + (1 – t) & gt; 0 + 0 + 0 = 0

(vì t8 ≥ 0; t2 ≥ 0 ⇒ t2 (1 – t3) ≥ 0)

+ xét t ≥ 1 ⇒ t3 ≥ 1 ⇒ t3 – 1 ≥ 0 và t – 1 ≥ 0.

t8 – t5 + t2 – t + 1 = t5. (t3 – 1) + t. (t – 1) + 1 ≥ 0 + 0 + 1 & gt; 0

thì với mọi t ≥ 0, thì t8 – t5 + t2 – t + 1 ≥ 1/2 & gt; 0 hoặc

Bài 6 trang 79 SGK Đại Số 10: Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất.

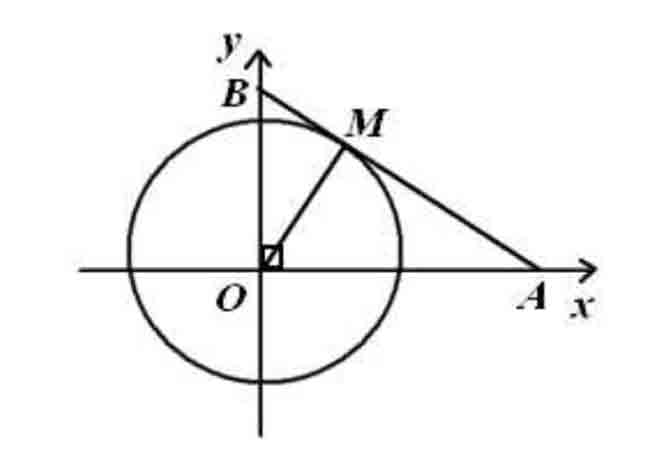
Lời giải:

– Gọi tiếp điểm là ab và chu vi tâm o và bán kính 1 m, ta có: om ⊥ ab.

áp dụng bất đẳng thức côsin, chúng ta có:

ma + mb ≥ 2√ma.mb = 2. √1 = 2

dấu “=” xuất hiện khi ma = mb = 1.

thì oa = √ (ma2 + mo2) = √2; ob = (om2 + mb2) = 2.

trong đó a, b thuộc tia ox và oy thì a (√2; 0); b (0; 2)

thì tọa độ là a (√2, 0) và b (0, √2).