Chuyên Đề Tỉ Lệ Thức Lớp 7 Violet, Sáng Kiến Kinh Nghiệm Toán Thcs

“Hướng dẫn học sinh lớp 7 giải bài tập áp dụng tính chất của dãy tỉ số bằng nhau”

Có thể bạn quan tâm

2. Lĩnh vực áp dụng sáng kiến: Giáo dục

3.Tác giả: Nguyễn Thị Mai; Giới tính: Nữ

Trình độ chuyên môn: Đại học sư phạm Toán

Chức vụ, đơn vị công tác: Giáo viên – Trường THCS Lê Danh Phương

gmail.com

Tỷ lệ áp dụng sáng kiến: 100%

4. Đơn vị áp dụng sáng kiến:

Tên đơn vị: Trường THCS Lê Danh Phương – Thị trấn Hưng Hà – Thái Bình

5. Thời gian áp dụng sáng kiến lần đầu: Năm học 2018 – 2019

II. BÁO CÁO MÔ TẢ SÁNG KIẾN

1. Tên sáng kiến: “Hướng dẫn học sinh lớp 7 giải bài tập áp dụng tính chất của dãy tỉ số bằng nhau”

2. Lĩnh vực áp dụng sáng kiến: Giảng dạy chuyên đề bồi giỏi môn Toán 7

3. Mô tả bản chất của sáng kiến:

3.1. Tình trạng giải pháp đã biết:

3.1.1 Hiện trạng trước khi áp dụng giải pháp mới

Trong quá trình công tác, làm nhiệm vụ giảng dạy đồng thời bồi dưỡng học sinh khá và giỏi môn toán 7, cùng với việc tham khảo ý kiến của các đồng nghiệp tôi nhận thấy :

v Chương trình SGK: Chưa xây dựng hoàn chỉnh về nội dung và phương pháp giải các bài toán về tính chất của dãy tỉ số bằng nhau chỉ mang tính chất giới thiệu chưa sâu. Trong khi đó giải toán về tính chất của dãy tỉ số bằng nhau là một dạng toán rất đa dạng và phong phú.

v Thực trạng về học sinh:

Ø Về hứng thú khi học dạng bài toán về tính chất của dãy tỉ số bằng nhau:

Học sinh được làm quen từ sớm với dạng toán này và hiệu quả học tập của các em chưa cao do học sinh chưa nắm được hết các phương pháp, kỹ năng giải một số dạng toán về tính chất của dãy tỉ số bằng nhau.

Đang xem: Chuyên đề tỉ lệ thức lớp 7 violet

Ø Về kỹ năng giải dạng bài toán về tính chất của dãy tỉ số bằng nhau:

– Học sinh tiếp thu bài máy móc, chưa linh hoạt, chỉ làm theo khuôn mẫu chứ chưa tự suy nghĩ để tự tìm cách giải.

– Học sinh chưa được rèn luyện giải nhiều về dạng bài nên khả năng nhận dạng bài tập và vận dụng phương pháp giải cho từng dạng bài tập chưa có. Dẫn đến học sinh lúng túng khi gặp các bài toán khó cần suy luận trong dạng này.

Ngoài ra những học sinh muốn tìm hiểu thêm còn lúng túng trong việc tìm tài liệu nghiên cứu vì tài liệu còn tản mạn, rải rác và còn mất nhiều thời gian.

Xuất phát từ tình hình thực tế cùng với kinh nghiệm trong quá trình giảng dạy, tôi đã làm sáng kiến “Hướng dẫn học sinh lớp 7 giải bài tập áp dụng tính chất của dãy tỉ số bằng nhau” với mong muốn học sinh phát hiện và sử dụng kiến thức đúng cách, có phương pháp giải đúng đắn và phát triển tư duy, sáng tạo.

Trong những năm học gần đây tôi đã triển khai dạng bài tập này trong các tiết luyện tập, đặc biệt trong công tác bồi dưỡng học sinh giỏi kết quả thu được rất khả quan. Qua bài kiểm tra khảo sát lớp 7A7 trong những năm gần đây như sau:

Kết quả kiểm tra đợt 1( khi chưa áp dụng sáng kiến ): Năm học 2017 – 2018

Lớp	Sĩ số	Điểm giỏi	Điểm khá	Điểm TB	Điểm yếu
SL	%	SL	%	SL	%	SL	%
7A7	34	5	14,7	18	52,94	10	29,41	1	2,95

Kết quả kiểm tra đợt 2( đã áp dụng sáng kiến ): Năm 2018 – 2019

Lớp	Sĩ số	Điểm giỏi	Điểm khá	Điểm TB	Điểm yếu
SL	%	SL	%	SL	%	SL	%
7A7	34	10	29,41%	21	61,76	03	8,83	0	0

Kết quả kiểm tra của lớp 7A7 ngày càng cao hơn là do học sinh đã biết phân tích đề bài và có phương pháp giải bài tập thích hợp.

3.2. Nội dung giải pháp đề nghị công nhận là sáng kiến:

3.2.1. Mục đích của giải pháp

Tôi nghiên cứu đề tài với mục đích là:

v Để đáp ứng nhu cầu tìm hiểu, học tập của giáo viên và học sinh. Với mục đích hệ thống, xây dựng cô đọng những phương pháp giải, hướng phát triển các bài toán, vận dụng kết quả của bài toán này vào giải quyết một số bài toán khác, nhằm

đưa ra một tài liệu cho học sinh, giáo viên tìm hiểu tham khảo thêm; giúp cho việc bồi dưỡng học sinh giỏi của giáo viên được tốt hơn. Tôi mong muốn trong công tác bồi dưỡng học sinh giỏi toán 7 các đồng nghiệp cùng trao đổi, cùng xây dựng để sáng kiến được hoàn thiện hơn, khai thác có hiệu quả hơn tác dụng của đề tài.

v Giúp các em hiểu rõ về chuyên đề tính chất của dãy tỉ số bằng nhau và phương pháp giải các dạng bài tập về chuyên đề đó.

– Tôi mong muốn phát triển tư duy logic, rèn kỹ năng giải toán cho học sinh, rèn tính linh hoạt, sáng tạo, khả năng liên tưởng và tạo hứng thú học tập tốt bộ môn.

– Làm cho học sinh yêu thích môn Toán hơn, mong muốn được tìm hiểu nghiên cứu sự thú vị và phong phú của môn Toán.

– Phát triển bài toán nhằm nâng cao năng lực, tư duy tự học của học sinh.

v Việc nghiên cứu đề tài này cho tôi một cơ hội để tự học, rút ra cho mình

những kinh nghiệm, những hiểu biết mới từ đó nâng cao khả năng chuyên môn, nghiệp vụ của bản thân.

3.2.2. Nội dung giải pháp

3.2.2.1 Tính mới của sáng kiến

v Phương pháp này phù hợp với mức độ tiếp thu của học sinh khá và giỏi.

Học sinh được kỹ năng vận dụng kiến thức, kích thích sự sáng tạo, tìm lời giải hay.

v Đề tài này là tài liệu tham khảo cho học sinh và các thầy cô giáo làm nhiệm vụ bồi dưỡng học sinh giỏi.

v
Việc vận dụng của đề tài không những giới hạn ở lớp 7 nói riêng cấp học THCS nói chung mà còn vận dụng ở nhiều cấp học cao hơn.

3.2.2.2. Cách giải pháp thực hiện

Xuất phát từ những vấn đề đã nêu ở trên tôi triển khai vấn đề này như sau:

1. Hệ thống những kiến thức cần ghi nhớ có liên quan đến các dạng toán.

2. Hệ thống và hướng dẫn học sinh cách giải các dạng bài tập đi từ dễ đến khó, từ đơn giản đến phức tạp.

Dạng 1: Tìm các giá trị của biến trong các tỉ lệ thức.

Dạng 2: Chia tỉ lệ

Dạng 3: Chứng minh tỉ lệ thức

3.2.2.3.

Xem thêm: Bộ Đề Thi Học Kì 2 Lớp 1 Theo Th Ôn Tập Phần Tiếng Việt Lớp 9 Học Kì 1 Violet

Cách giải pháp thực hiện cụ thể

1. Hệ thống những kiến thức cần ghi nhớ có liên quan đến các dạng toán

tính chất của dãy tỉ số bằng nhau

* Từ

suy ra

* Từ dãy tỉ số bằng nhau

ta suy ra

( giả thiết các tỉ số đều có nghĩa).

* Nếu có n tỉ số bằng nhau (

thì

(Nếu đặt dấu “-“ trước số hạng trên của tỉ số nào thì cũng đặt dấu “-“ trước số hạng dưới của tỉ số đó).

* Tính chất của dãy tỉ số bằng nhau cho ta một khả năng rộng rãi để từ một số tỉ số bằng nhau cho trước, ta lập được những tỉ số mới bằng các tỉ số đã cho, trong đó số hạng trên hoặc số hạng dưới của nó có dạng thuận lợi nhằm sử dụng các dữu kiện của bài toán.

2. Hệ thống và hướng dẫn học sinh cách giải các dạng bài tập đi từ dễ đến khó, từ đơn giản đến phức tạp.

Dạng I: Tìm các giá trị của biến trong các tỉ lệ thức.

* Tính chất của dãy tỉ số bằng nhau:

– Tính chất: Ta luôn có

– Tính chất mở rộng:

(Giả thiết các tỉ số đều có nghĩa)

Xem Thêm : Blog Nguyễn Văn Thùy – #Ad Điềm Giải Tích C1 =)) Ai Qua Điểm

Ví dụ 1: Tìm x, y biết:

và

Giải:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy

;

Ví dụ 2: Tìm x, y biết:

và

Phân tích đề bài: Ta phải viết tỉ lệ thức dưới dạng dãy tỉ số bằng nhau.

Giải:

Ta có:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy

;

Ví dụ 3: Tìm x, y, z biết:

và

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy:

;

;

Nhận xét: Ở ví dụ 1 và ví dụ 3 ta áp dụng ngay được tính chất dãy tỉ số bằng nhau. Trong thực tế nhiều bài tập phải qua quá trình biến đổi mới có thể đưa được về dạng để áp dụng được tính chất dãy tỉ số bằng nhau. Sau đây là một số dạng và cách biến đổi.

Ví dụ 4: Tìm x, y, z biết:

và.

Phân tích đề bài: Để áp dụng được tính chất dãy tỉ số bằng nhau, ta phải biến đổi dãy tỉ số sao cho hệ số của x, y, z ở các tử của dãy tỉ số bằng hệ số của x, y, z trong đẳng thức, bằng cách áp dụng tính chất cơ bản của phân số. Cụ thể nhân cả tử và mẫu của tỉ số

với 2 và nhân cả tử và mẫu của tỉ số

với 3 rồi áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.

Giải:

Ta có:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy

Ví dụ 5: Tìm x, y, z biết: và

Phân tích đề bài: Cách làm giống ví dụ 4

Giải:

Ta có:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy:

;

;

Nhận xét: Ở bài này ta còn có thể dùng phương pháp đặt ẩn phụ.

Ví dụ 6: Tìm x, y biết: và

Ở bài này, ta viết đẳng thức về dạng dãy tỉ số bằng nhau sau đó vận dụng cách làm ở ví dụ 4

Ví dụ 7: Tìm x, y, z biết: và

Phân tích đề bài: Ta đưa dãy đẳng thức về dạng dãy tỉ số bằng nhau sao cho hệ số của x, y, z trong dãy tỉ số bằng nhau bằng bằng 1.

Cách làm chia các tích cho 12 vì:

sau đó làm như ví dụ 3

Giải:

Từ:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy

;

;

Ví dụ 8: Tìm x, y biết: và

Phân tích đề bài: Để áp dụng được tính chất dãy tỉ số bằng nhau, ta phải biến đổi dãy tỉ số bằng nhau làm xuất hiện tích x.y bằng cách lập luận để chứng tỏ rồi nhân hai vế của hai tỉ số với x. Thay vào rồi tính.

Giải:

Vì

Nhân cả hai vế của

với x ta được:

Nếu

Nếu

Vậy:

;

hoặc

;

Nhận xét: Ở bài này ta còn có thể dùng phương pháp đặt ẩn phụ.

Ví dụ 9: Tìm x, y, z biết:

và

Phân tích đề bài: Để áp dụng được tính chất của dãy tỉ số bằng nhau, ta phải biến đổi dãy tỉ số bằng nhau làm xuất hiện tích x.y.z bằng cách lập luận chứng tỏ rồi biến đổi dãy tỉ số bằng nhau về dạng

Sau đó làm tương tự ví dụ 8.

Ví dụ 10: Tìm x, y, z biết: ; và

Phân tích đề bài: Đưa hai dãy tỉ số ; về một dãy ba tỉ số bằng nhau bằng cách biến đổi y ở hai dãy tỉ số về cùng mẫu sau đó làm giống ví dụ 4

Giải:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy

;

;

Ví dụ 11: Tìm x, y, z biết:

Giải:

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

(vì

Do đó

Thay kết quả này vào đề bài ta được:

Tức là

Vậy

Ví dụ 12: Tìm x, y, z biết: ; (1) và

Phân tích đề bài: Đưa hai dãy tỉ số ; về một dãy ba tỉ số bằng nhau giống ví dụ 8 rồi lập phương các tỉ số để xuất hiện

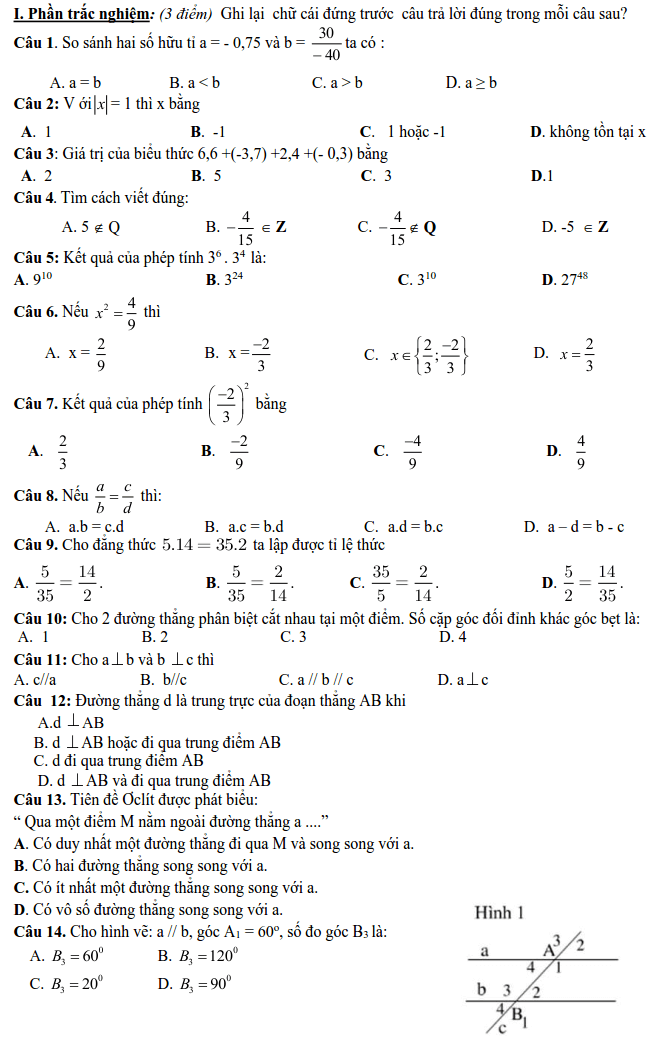
sau đó áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.

Giải:

Ta có:

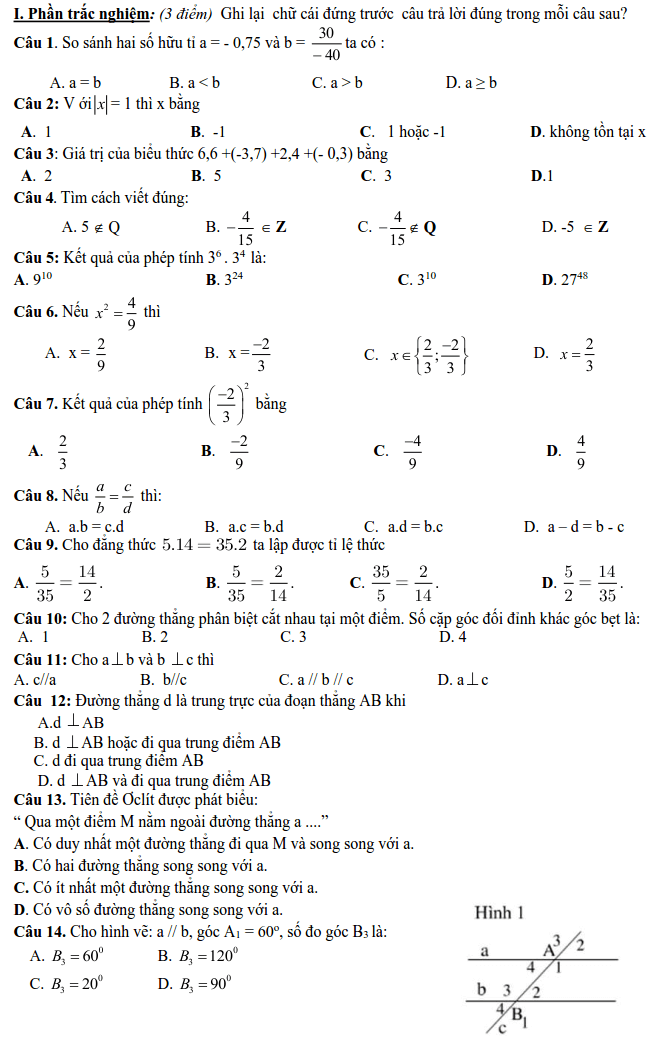
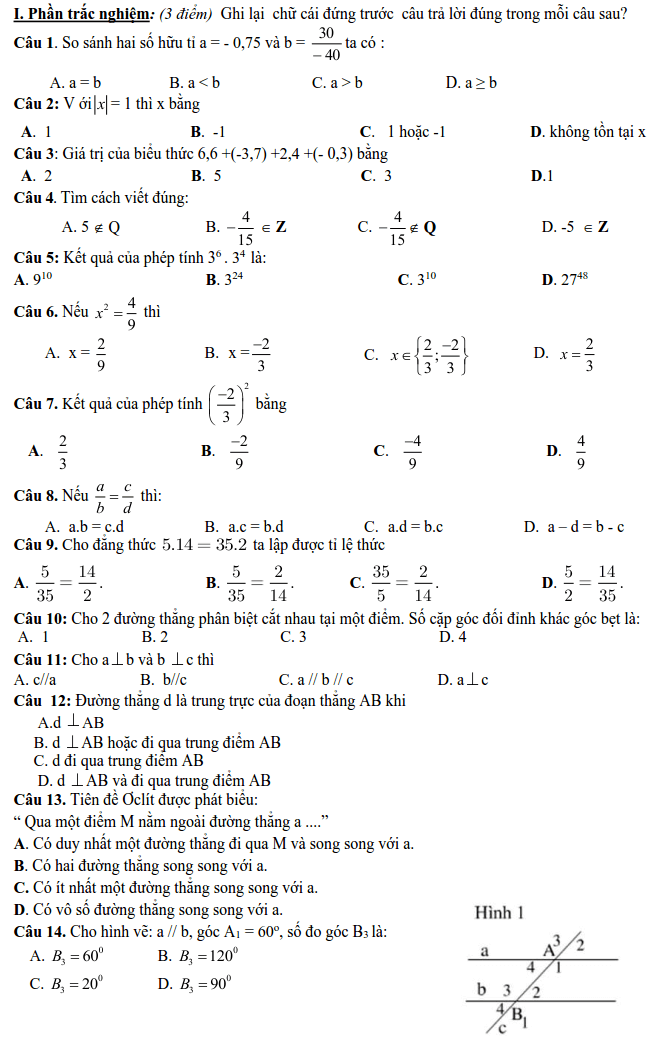
Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy:

;

và

Ví dụ 13: Cho

và ;

. Tính: b, c.

Phân tích đề bài: Vì ta áp dụng ngay tính chất dãy tỉ số bằng nhau để tìm giá trị của dãy tỉ số này rồi từ đó tìm ra giá trị của a, b, c.

Giải:

Vì

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Mà

Vậy:

Bài tập áp dụng:

Bài 1: Tìm x, y biết.

và

và

và

d) và

e) và

và

Bài 2: Tìm x, y, z biết.

Xem Thêm : Thư Viện Đề Thi Thử Thpt Quốc Gia 2018 Môn Toán Violet Archives

và

;

và

và

và

và

Bài 3: Tìm x, y, z biết.

Xem thêm: 121 Bai Tap Tieng Anh 6 Thi Diem, Bài Tập Tiếng Anh 6 Thí Điểm

;

và

b) và

và

Bài 4: Tìm x biết.

Bài 5: Tìm các số

biết.

và

Dạng II: Chia tỉ lệ.

I – Một số chú ý:

1) x, y, z tỉ lệ thuận với a, b, c

( Hay

)

2) x, y, z tỉ lệ nghịch với a, b, c

( Hay

)

II – Bài tập:

Ví dụ 1: Chu vi của hình chữ nhật bằng 28 dm. Tính độ dài mỗi cạnh, biết rằng chúng tỉ lệ với 3; 4.

Phân tích đề bài: Trong hình chữ nhật có hai kích thước là chiều dài và chiều rộng (còn được gọi là hai cạnh của hình chữ nhật) chiều rộng thì ngắn hơn chiều dài. Hai cạnh của chúng tỉ lệ với 3; 4 vậy cạnh ngắn tỉ lệ với 3 còn cạnh dài tỉ lệ với 4.

Nếu gọi hai cạnh của hình chữ nhật là a và b . Vì hai cạnh hình chữ nhật ti lệ với 3 và 4 nên ta có:

Chu vi hình chữ nhật là

nên ta có:

Như vậy ta đã đưa bài toán về dạng bài áp dụng tính chất dãy tỉ số bằng nhau.

Giải:

Gọi hai cạnh của hình chữ nhật là a (dm) và b (dm)

Theo bài ra ta có:

và

Từ

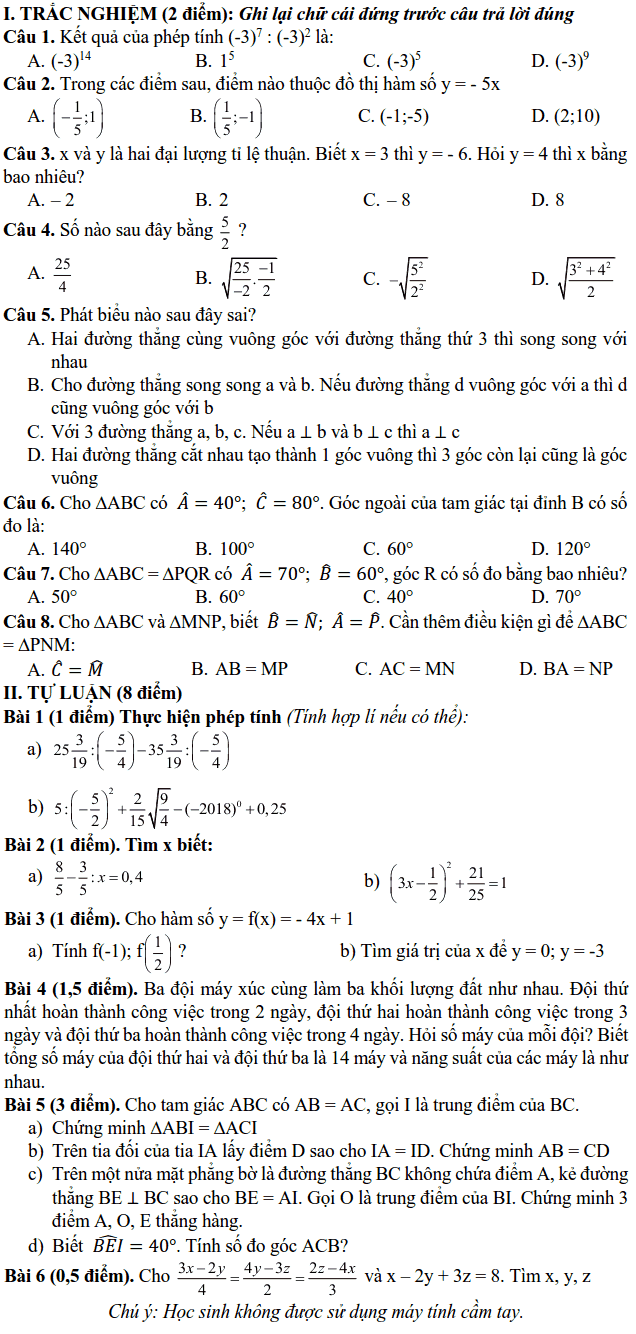
Áp dụng tính chất dãy tỉ số bằng nhau ta có:

(TMĐK);

(TMĐK).

Vậy độ dài hai cạnh hình chữ nhật là 6 dm và 8 dm.

Ví dụ 2: Cho tam giác ABC có các góc A, B, C tỉ lệ với 7: 5: 3. Các góc ngoài tương ứng tỉ lệ với các số nào.

Phân tích đề bài: Nếu gọi ba góc của tam giác ABC lần lượt là: .

Vì ba góc tỉ lệ với 7: 5: 3 nên ta có

Tổng ba góc của một tam giác bằng

nên ta có:

Từ đó ta tìm được số đo các góc của tam giác,

Mà tổng của góc ngoài và góc trong tại một đỉnh của tam giác bù nhau.

Giải:

Gọi ba góc trong và góc ngoài của tam giác ABC lần lượt là: và

Theo bài ra ta có: và .

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy các góc ngoài tương ứng tỉ lệ với:

Ví dụ 3: Có 16 tờ giấy bạc loại 2000 đồng, 5000 đồng và 10000 đồng, trị giá mỗi loại tiền trên đều bằng nhau. Hỏi mỗi loại có mấy tờ.

Phân tích đề bài:

Gọi số tờ tiền loại 2000 đồng, 5000 đồng và 10000 đồng lần lượt là a, b, c

Vì giá trị mỗi loại tiền đều bằng nhau nên ta có:

Có 16 tờ giấy bạc các loại nên:

Giải:

Gọi số tờ tiền của loại 2000 đồng, 5000 đồng và 10000 đồng lần lượt là a, b, c (

)

Theo bài ra ta có: và

Từ:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

;

(TMĐK)

Vậy số tiền loại 2000 đồng, 5000 đồng, 10000 đồng lần lượt là 10 tờ, 4 tờ và 2 tờ.

Ví dụ 4: Ba đội công nhân I, II, III phải vận chuyển tổng cộng 1530 kg hàng từ kho theo thứ tự đến ba địa điểm cách kho 1500m, 2000m, 3000m. Hãy phân chia số hàng cho mỗi đội sao cho khối lượng hàng tỉ lệ nghịch với khoảng cách cần chuyển.

Phân tích đề bài: Vì phân chia số hàng cho mỗi đội sao cho khối lượng hàng tỉ lệ nghịch với khoảng cách cần chuyển nên ta có:

Tổng số hàng cần chuyển đến ba kho là 1530 nên ta có: .

Giải:

Gọi số lượng hàng chuyển tới ba kho lần lượt là a, b, c

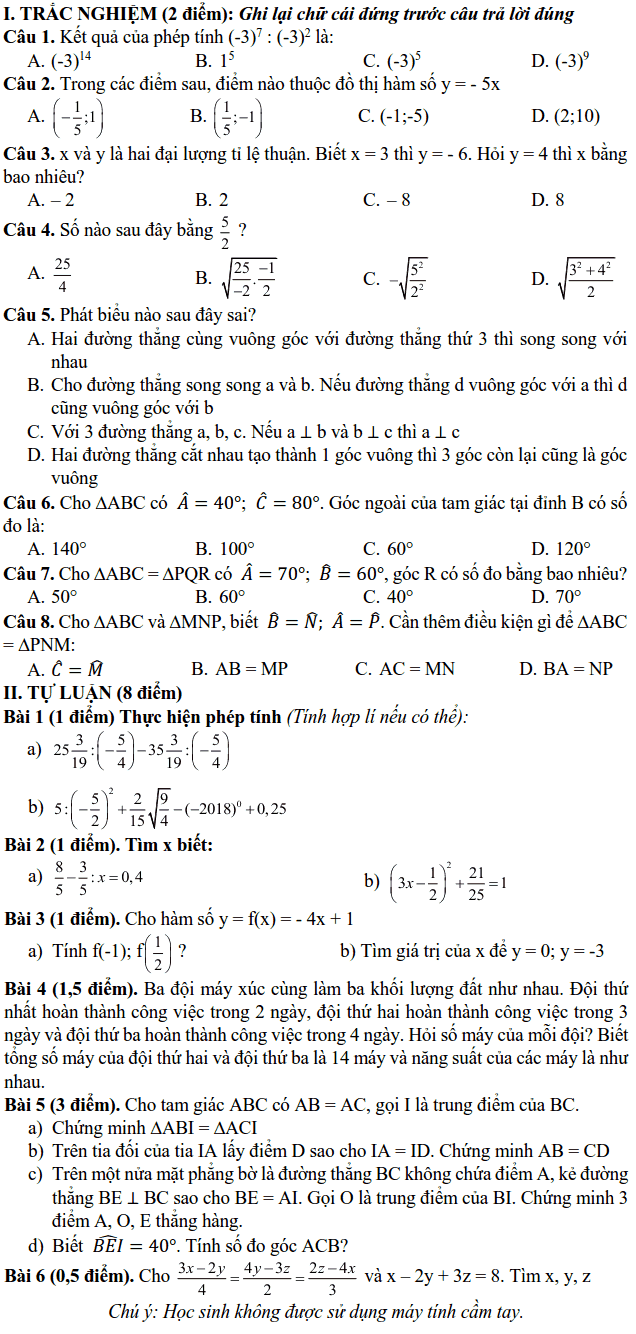
Theo bài ra ta có: và

Từ:

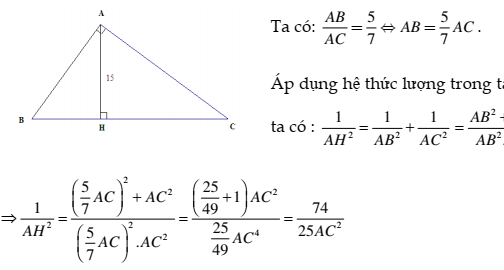
Áp dụng tính chất dãy tỉ số bằng nhau ta có:

(TMĐK)

(TMĐK)

(TMĐK)

Vậy số hàng cần chuyển tới ba kho A, B, C lần lượt là: 680 tạ, 510 tạ, 340 tạ.

Ví dụ 5: Một lớp học có 35 em, sau khảo sát chất lượng số học sinh được xếp thành ba loại: Giỏi, khá và trung bình. Số học sinh giỏi và khá tỉ lệ với 2 và 3, số học sinh khá và trung bình tỉ lệ với 4 và 5. Tính số học sinh mỗi loại.

Phân tích đề bài: Nếu gọi số học sinh giỏi, khá, trung bình của lớp đó lần lượt là: a, b, c